반응형
Outline
- Bias-variance tradeoff & Cross-validation
Performance metrics for classification
BIAS-VARIANCE TRADEOFF
1.1 Underfitting and Overfitting

1.2 Bias and Variance
- 학습 방법을 선택할 때 항상 경쟁 관계에 있는 두 가지 요소가 있습니다.
- 바로 편향(Bias)과 분산(Variance)입니다.
- 편향은 복잡한 문제를 훨씬 단순화된 방식으로 모델링함으로써 발생하는 오류를 의미합니다.
- 예를 들어, 데이터의 복잡한 패턴이나 관계를 충분히 반영하지 못하고 너무 간단한 모델을 사용하게 될 경우 높은 편향이 발생할 수 있습니다.
- 분산은 다른 훈련 데이터 세트를 사용했을 때 추정치가 얼마나 변할지를 나타냅니다.
- 즉, 모델이 훈련 데이터에 너무 민감하게 반응하여 작은 변화에도 예측이 크게 달라질 경우 높은 분산을 가지게 됩니다.
- 이 두 요소는 서로 상충 관계에 있습니다.
- 즉, 편향을 줄이기 위해 모델을 복잡하게 만들면 분산이 증가할 수 있고, 반대로 분산을 줄이기 위해 모델을 단순화하면 편향이 증가할 수 있다.
- 따라서, 학습 방법을 선택할 때는 이러한 편향과 분산 사이의 균형을 고려하여 최적의 모델을 찾아야 합니다.
1.3 Bias-Variance Trade-off

- Bias-Variance Trade-off는 모델의 기대되는 테스트 MSE(Mean Squared Error, 평균 제곱 오차)가 다음과 같이 분해될 수 있다는 것을 의미합니다:
- Bias(편향): 모델이 실제 데이터를 얼마나 잘 대표하지 못하는지에 대한 오차입니다.
- 편향이 높은 모델은 데이터의 복잡성을 충분히 포착하지 못하며, 너무 단순화된 가정으로 인해 발생합니다.
- Variance(분산): 훈련 데이터 세트의 작은 변화에 모델이 얼마나 민감하게 반응하는지에 대한 척도입니다.
- 분산이 높은 모델은 훈련 데이터에 너무 과하게 적합되어 새로운 데이터에 대해 일반화하는 능력이 떨어집니다.
- 오차(Error): 데이터 자체의 노이즈로 인한 오차로, 이는 모델로는 제어할 수 없는 부분입니다.
- 이러한 관점에서, 모델이 더 복잡해질수록 편향은 감소하지만 분산은 증가하며, 기대되는 테스트 오류는 증가하거나 감소할 수 있습니다!
- 따라서, 모델을 선택할 때는 편향과 분산 사이의 균형을 잘 맞추는 것이 중요합니다.
- 너무 단순한 모델은 데이터를 충분히 학습하지 못할 수 있고, 너무 복잡한 모델은 훈련 데이터에 과적합되어 새로운 데이터에 대한 예측이 부정확해질 수 있습니다.
- 이러한 이유로, 모델의 복잡도를 적절히 조절하는 것이 중요합니다.
1.4 A Fundamental Picture
- 일반적으로, 훈련 오류는 항상 감소할 것입니다.
- 그러나, 테스트 오류는 처음에는 감소하다가(편향 감소가 우세할 때) 이후에는 다시 증가하기 시작할 것입니다(분산 증가가 우세해질 때).
- 이는 과적합(overfitting) 문제와 관련이 있습니다.
- 모델이 너무 복잡하거나 유연하면, 훈련 데이터에 대해서는 매우 잘 작동할 수 있지만, 새로운 데이터에 대해서는 오히려 성능이 떨어질 수 있습니다.
- 이는 모델이 훈련 데이터의 노이즈까지 학습하여, 훈련 데이터에 과도하게 최적화되었기 때문입니다.
- 따라서, 모델 선택 시, 훈련 오류와 테스트 오류의 관계를 이해하고, 적절한 복잡도의 모델을 선택하는 것이 중요합니다.

Cross-validation
1.5 Cross-validation (교차검증)
- 교차검증은 모델의 유효성을 검증하는 방법 중 하나로, 내부 검증(internal validation) 및 외부 검증(external validation)으로 나뉩니다.
- 외부 검증은 모델을 완전히 새로운 데이터셋에서 검증하는 것을 의미합니다.
- 이는 모델이 다른 데이터셋에서 얼마나 잘 작동하는지 평가하기 위해 사용됩니다.
- 내부 검증은 현재 데이터셋을 사용하여 모델을 검증하는 방법으로, 교차검증(cross-validation)이 여기에 해당됩니다.
- 교차검증은 전체 데이터셋을 여러 부분으로 나누고, 이 중 일부를 훈련 데이터로, 나머지를 테스트 데이터로 사용하여 모델을 여러 번 검증합니다.
- 교차검증을 사용하는 경우는 다음과 같습니다:
- 최적의 모델이나 하이퍼파라미터 설정을 선택할 때 모델이 훈련 데이터에 과적합(over-fit)되지 않고 새로운 데이터셋에서 좋은 예측 성능을 보일 것임을 증명하고 싶을 때 교차검증을 통해 모델의 일반화 능력을 더 정확하게 평가할 수 있고, 다양한 데이터셋에 대한 모델의 성능을 검증할 수 있습니다.
- 이는 모델이 실제 상황에서도 안정적으로 작동할 수 있음을 보장하는 중요한 과정입니다.
1.6 Cross-validation method
- Holdout validation
- K-fold cross validation
- Leave-one-out validation
1.7 Holdout (or Test-set) validation

- 홀드아웃(또는 테스트 세트) 검증은 데이터를 훈련 세트와 테스트 세트로 나누어 모델을 평가하는 기본적인 방법입니다.
- 이 방식은 데이터가 충분하지 않을 때 자주 사용되지만, 몇 가지 단점이 있습니다.
- 데이터를 어떻게 나누느냐에 따라 결과가 민감하게 달라질 수 있습니다.
- 즉, 데이터의 분할 방식에 따라 모델의 성능 평가가 크게 변동될 수 있습니다.
- 여전히 과적합(Overfitting)의 위험이 있습니다.
- 특히, 테스트 세트에 대해서만 모델이 잘 작동하고 일반적인 경우에는 잘 작동하지 않을 수 있습니다.
- 따라서, 홀드아웃 검증 방법은 데이터가 충분히 많지 않거나, 데이터 분할에 따른 성능 변동을 최소화할 수 있는 경우에 적합합니다.
- 하지만, 과적합을 피하고 모델의 일반화 능력을 더 정확히 평가하기 위해서는 교차 검증과 같은 다른 방법들을 고려하는 것이 좋습니다.
1.8 K-fold cross validation
- K-겹 교차 검증은 데이터 세트를 K개의 서브셋으로 나누고, 홀드아웃 방법을 K번 반복하는 절차입니다.
- 각 반복에서 하나의 서브셋이 테스트 세트로 사용되며, 나머지 서브셋들은 훈련에 사용됩니다.
- 이 과정을 통해 얻은 각각의 성능을 평균내어 모델의 전반적인 성능을 평가합니다.
- 이 방법을 통해 모델이 데이터의 다양한 부분에서 얼마나 잘 작동하는지를 더 정확하게 평가할 수 있으며, 모델의 일반화 능력에 대한 더 안정적인 추정치를 얻을 수 있다.
1.9 Example: 5-fold CV

1.10 K-fold CV
- K-fold Cross-Validation (K-겹 교차 검증)은 모델의 성능을 평가하고 최적의 하이퍼파라미터 값을 찾기 위해 널리 사용되는 방법입니다.
- 이 방법은 전체 데이터 세트를 K개의 동일한 크기를 가진 부분 집합으로 나눈 다음, 하나의 부분 집합을 테스트 데이터로, 나머지 K-1개의 부분 집합을 합쳐서 훈련 데이터로 사용합니다.
- 이 과정을 K번 반복하며, 각 반복마다 다른 부분 집합을 테스트 데이터로 사용합니다.
- K-fold 교차 검증의 주요 단계는 다음과 같습니다:
- K번의 시행(trial)에 걸쳐 각각의 오류율(또는 정확도 측정)을 계산합니다.
- 모든 K번의 시행에 대한 오류율(또는 정확도)의 평균을 계산하여 모델의 성능을 평가합니다.
- 이 방법은 모델 튜닝, 즉 최적의 하이퍼파라미터 값을 찾는 데 주로 사용됩니다.
- 최적의 하이퍼파라미터 값을 찾은 후에는 완전한 훈련 데이터 세트를 사용하여 모델을 재훈련하고 독립적인 테스트 데이터 세트를 사용하여 최종 성능 추정치를 얻습니다.

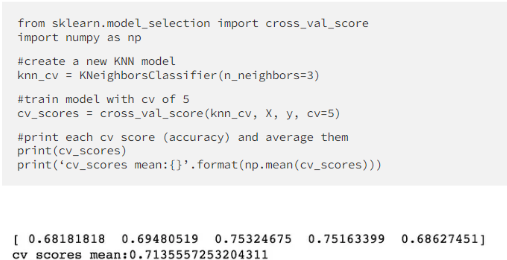
1.11 Example: KNN 5-fold CV accuracy
1.12 CV-based model selection
- 교차 검증 기반 모델 선택의 예로 k-NN(k-Nearest Neighbors)에서 "k"를 선택하는 과정을 들 수 있습니다.
- 1단계: 여러 다른 모델 클래스에 대해 10-폴드 교차 검증(CV) 오류를 계산합니다.
- 예를 들어, k-NN 모델에서 서로 다른 'k' 값(예: 1, 3, 5, 7, 9, 11)에 대한 10-폴드 교차 검증을 수행하여 각각의 평균 오류를 계산합니다. 2단계: 가장 좋은 CV 점수를 낸 모델 클래스를 전체 데이터로 다시 학습시킵니다.
- 이렇게 학습된 모델이 최종적으로 사용할 예측 모델입니다.
- 이 과정을 통해 여러 후보 중에서 최적의 모델 파라미터를 선택하고, 해당 파라미터로 모델을 재학습시켜 최종 모델을 구축할 수 있습니다.
- 이 방법은 데이터의 여러 부분 집합을 활용하여 모델의 성능을 평가하므로, 단순히 한 번의 학습과 검증으로 모델을 선택하는 것보다 더 신뢰할 수 있는 모델을 구축하는 데 도움이 됩니다.

1.13 K-fold CV advantages
- K-fold 교차 검증의 장점:
- 데이터가 어떻게 나뉘었는지가 덜 중요합니다:
- K-fold 교차 검증은 데이터를 무작위로 K개의 그룹으로 나누며, 이로 인해 데이터 분할 방법이 결과에 미치는 영향이 줄어듭니다.
- 모든 데이터 포인트가 정확히 한 번은 테스트 세트에 포함되고, K-1 번은 훈련 세트에 포함됩니다:
- 이는 모든 데이터가 모델 학습과 검증에 고르게 사용되어, 모델의 일반화 능력을 평가하는 데 도움이 됩니다.
- 홀드아웃 방법보다 낮은 변동성 추정치를 제공합니다:
- K-fold 교차 검증은 여러 번의 학습과 검증을 거치기 때문에, 단일 홀드아웃 테스트에 비해 더 안정적이고 신뢰할 수 있는 성능 추정치를 제공합니다.
- 일반적으로 사용되는 선택은 10-fold 또는 5-fold 교차 검증입니다:
- 이는 실제 적용에서 균형 잡힌 성능 평가와 계산 비용 사이의 좋은 타협점을 제공하기 때문입니다.
- 이와 같이, K-fold 교차 검증은 데이터를 고르게 활용하고, 모델의 성능을 보다 정확하고 안정적으로 평가할 수 있도록 해주는 방법입니다.
1.14 Improvement
- 층화 K-fold 교차 검증(Stratified K-fold Cross-Validation)은 표준 K-fold 교차 검증에 비해 약간의 개선을 제공합니다.
- 특히 클래스 비율이 불균형한 경우에 유용합니다.
- 이 방법은 각 fold 내에서 클래스 레이블의 비율을 유지합니다.
- 일반 K-fold 교차 검증에서는 데이터를 단순히 K개의 fold로 나눕니다.
- 이 경우, 불균형한 클래스 비율을 가진 데이터셋에서는 일부 fold에서 특정 클래스의 샘플이 과도하게 많거나 적을 수 있습니다.
- 반면, 층화 K-fold 교차 검증에서는 전체 데이터셋의 클래스 비율을 각 fold에서도 유지하려고 합니다.
- 즉, 각 fold가 전체 데이터셋의 축소된 대표 버전이 되도록 합니다.
- 이 방법은 모델의 학습과 검증 과정에서 클래스 비율의 불균형으로 인한 편향을 줄여줍니다.
- 따라서, 층화 K-fold 교차 검증은 특히 클래스 비율이 중요한 상황에서 더 정확한 모델 성능 평가를 가능하게 합니다.
1.15 Leave-One-Out CV (LOOCV)
- Leave-One-Out 교차 검증(LOOCV)은 K-겹 교차 검증(K-fold CV)의 특별한 경우입니다.
- 여기서 K는 훈련 샘플의 수, 즉 n과 같습니다.
- 이 방법은 매우 작은 데이터셋을 다룰 때 추천됩니다.
- LOOCV에서는 데이터셋의 각 샘플을 한 번씩 테스트 데이터로 사용하고, 나머지 샘플들을 훈련 데이터로 사용합니다.
- 이 과정을 모든 샘플에 대해 반복하면서, 모델의 성능을 평가합니다.
- 이 방법은 데이터셋의 모든 샘플을 최대한 활용하기 때문에 작은 데이터셋에 대한 모델의 성능을 정확하게 평가할 수 있습니다.
- 그러나 LOOCV는 계산 비용이 매우 높은 방법입니다.
- 데이터셋의 샘플 수만큼 모델을 훈련시켜야 하기 때문에, 대규모 데이터셋에는 부적합할 수 있습니다.
- 그럼에도 불구하고, 매우 작은 데이터셋에서는 모델의 성능을 평가하기에 좋은 방법 중 하나입니다.
1.16 Leave-One-Out Cross Validation

1.17 LOOCV
- LOOCV(Leave-One-Out Cross-Validation)는 데이터 샘플 중 하나를 테스트 데이터로 남겨두고 나머지를 훈련 데이터로 사용하여 모델을 학습하는 방법입니다.
- 이 과정을 모든 데이터 샘플에 대해 반복하여, 즉 각 샘플을 한 번씩 테스트 데이터로 사용하여 모델의 성능을 평가합니다. 각 실행에서의 성능을 요약하여 모델의 전체 성능을 평가합니다.
- LOOCV는 모델 평가 결과가 좋은 편이지만, 계산 비용이 매우 높습니다.
- 만약 데이터 포인트가 n개 있다면, 학습 알고리즘을 n회 실행해야 하며, 이는 알고리즘 실행 시간에 n을 곱한 것과 같습니다.
- 따라서, LOOCV는 데이터 포인트의 수가 많은 경우 매우 시간이 많이 소요될 수 있습니다.
- 그러나 이 방법은 모델의 성능을 정확하게 평가할 수 있다는 장점이 있습니다.
반응형


