Content
Introduction to supervised learning approachData split in supervised learning- Classification algorithms
KNN & distance measuresDecision treeRandom Forest, Ensemble approach- SVM
3. Classification algorithms - SVM( SUPPORT VECTOR MACHINE )
SVM: Content
1. Linear SVM
2. Linear SVM: non-separable case
3. Non-linear SVM – Kernel trick
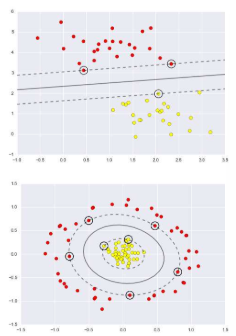
3.1 SVM: Introduction
SVM, 즉 Support Vector Machine은 1960년대 Vapnik에 의해 시작된 통계학습이론을 기반으로 하는 학습 방법입니다. 간단한 SVM은 복잡한 특징을 갖는 정교한 신경망을 손글씨 인식 작업에서 능가할 수 있었습니다. 그러나 현재는 많은 애플리케이션에서 심층 신경망이 SVM을 능가하는 성능을 보여주고 있습니다. SVM의 해결책은 입력 공간과 비선형적으로 관련된 고차원 특징 공간에서의 간단한 기하학적 해석을 가지고 있습니다. 이는 고차원에서의 데이터를 분류하기 위해 최적의 경계면(결정 경계)을 찾는 방식으로, 이 경계면은 서로 다른 분류에 속하는 데이터들 사이의 마진을 최대화하는 것을 목표로 합니다. 이러한 접근 방식으로 SVM은 높은 분류 성능과 함께 강력한 이론적 기반을 제공합니다.
3.2 Support Vector Machines
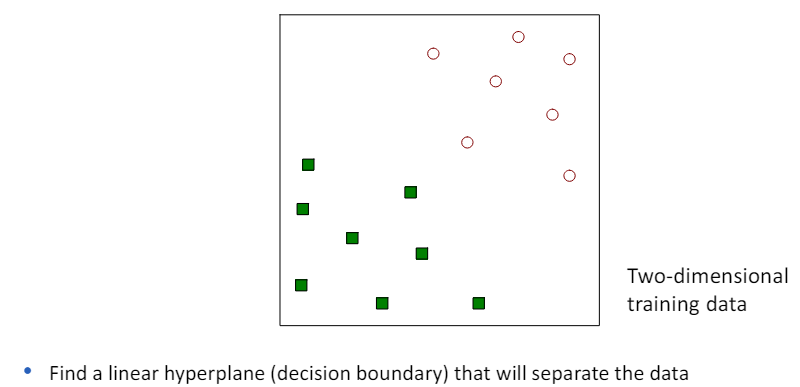
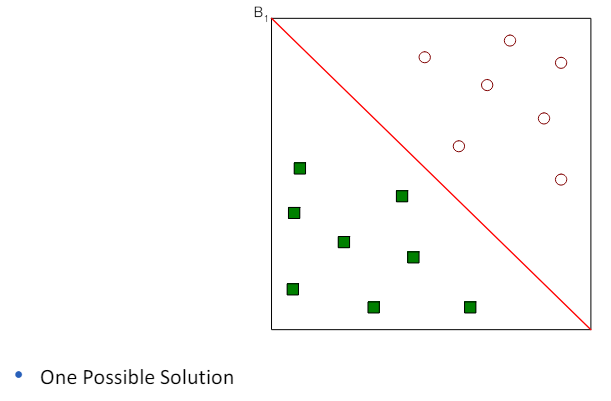
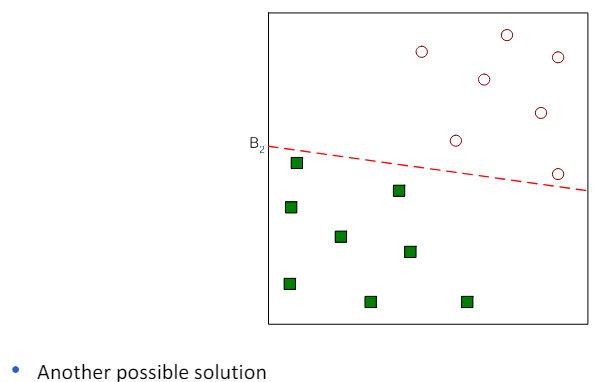
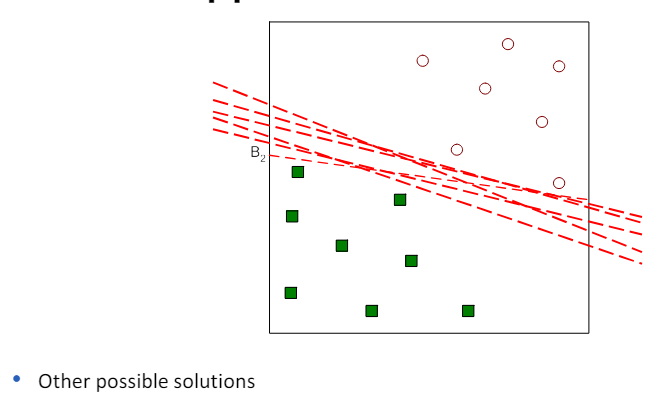
3.3 Linear SVM: separable case
- 선형 SVM(Linear SVM)은 이진 분류 문제에 대해 설명할 때 사용되는 모델.
- 여기서 우리는 N개의 훈련 샘플 (xi, yi), i=1,...,n을 고려하며, 각 샘플은 특성 벡터 xi=(xi1,xi2,...,xid)^t와 클래스 라벨 yi(값이 -1 또는 1)으로 구성.
- 선형 분류기가 존재하고, 이 분류기는 훈련 샘플을 완벽하게 두 클래스로 분리할 수 있다고 가정.
- 이 경우, 선형 SVM의 목표는 이 두 클래스를 분리하는 최적의 선형 결정 경계(결정 평면)를 찾는 것입니다.
- 이 결정 경계는 두 클래스 사이의 마진(클래스 간 경계와 가장 가까운 훈련 샘플 사이의 거리)을 최대화하는 선(또는 평면)입니다.
- 간단히 말해, 선형 SVM은 두 클래스를 분리하는 가장 좋은 '선'을 찾는 방법으로, 이 선은 두 클래스 사이에서 가능한 가장 큰 거리를 가지는 선을 의미.

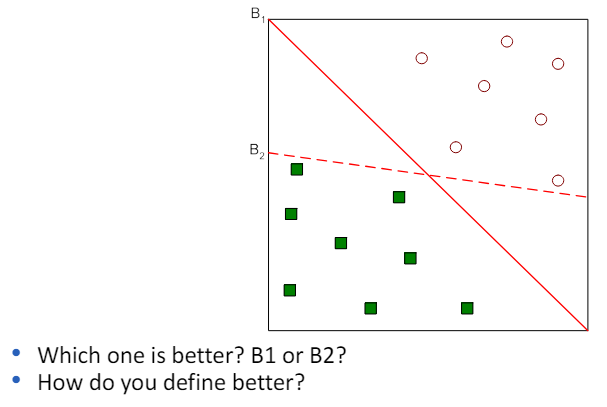
3.4 Linear SVM: max-margin idea

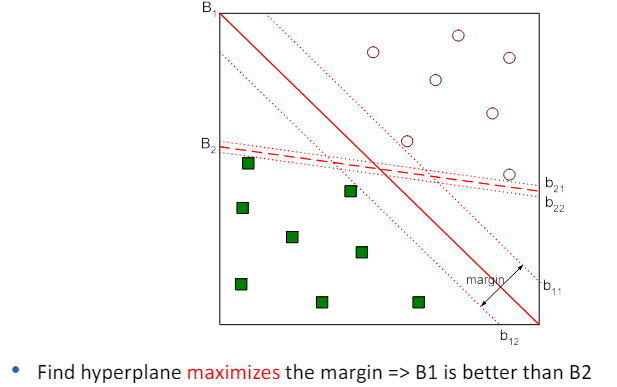
3.5 How to compute the margin

3.6 Learning linear SVM
- 선형 SVM (Support Vector Machine) 학습 학습 단계: 훈련 데이터로부터 파라미터 w와 b를 추정함 선형 SVM은 분류 문제, 특히 이진 분류 문제를 해결하기 위한 모델입니다.
- 학습 단계에서는 훈련 데이터를 사용하여 최적의 결정 경계를 찾는 것이 목표입니다.
- 이 결정 경계는 데이터를 두 클래스로 나누는 직선(또는 초평면)입니다.
- 학습 과정에서 SVM은 두 클래스 사이의 마진(결정 경계와 가장 가까운 훈련 샘플 간의 거리)을 최대화하는 결정 경계를 찾습니다.
- 이를 위해, 선형 SVM은 다음과 같은 최적화 문제를 해결하여 파라미터 w(결정 경계의 방향을 결정하는 벡터)와 b(결정 경계의 위치를 결정하는 스칼라)를 추정합니다.
- [ \min_{w,b} \frac{1}{2} |w|^2 ] [ \text{subject to } y_i (w \cdot x_i + b) \geq 1, \text{ for all } i ] 여기서 (x_i)는 훈련 샘플, (y_i)는 해당 샘플의 클래스 레이블(-1 또는 1)을 나타냅니다.
- 이 최적화 문제를 해결함으로써, SVM은 데이터를 가장 잘 분류하는 w와 b를 찾아내며, 이를 통해 새로운 데이터에 대한 분류 결정을 내릴 수 있게 됩니다.
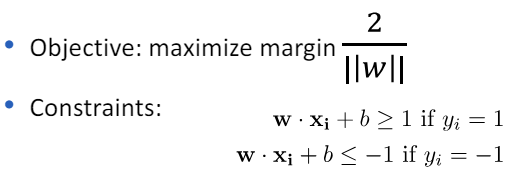
3.7 SVM as an optimization problem

- SVM(서포트 벡터 머신)을 최적화 문제로서 접근하는 것은 제약이 있는 (볼록한) 최적화 문제로 볼 수 있습니다. 이 문제를 해결하기 위한 수치적 접근 방법으로는 쿼드라틱 프로그래밍(quadratic programming)과 라그랑주 승수법(Lagrange multiplier method) 등이 있습니다. 쿼드라틱 프로그래밍: 이 방법은 목적 함수가 2차 형태이고 제약 조건이 선형인 최적화 문제를 해결하는 데 사용됩니다. SVM의 최적화 문제는 이러한 형태를 띠기 때문에, 쿼드라틱 프로그래밍을 통해 최적의 결정 경계를 찾는 매개변수 (w)와 (b)를 찾을 수 있습니다. 라그랑주 승수법: 이 방법은 제약 조건이 있는 최적화 문제를 제약 조건이 없는 문제로 변환하여 해결합니다. 라그랑주 승수법을 사용하면, SVM의 목적 함수에 제약 조건을 통합하여 라그랑주 함수를 구성하고, 이 함수를 최대화하는 (w), (b), 그리고 라그랑주 승수 (\alpha)를 찾음으로써 최적의 해를 얻을 수 있습니다. 이러한 방법들을 통해, SVM은 주어진 데이터에 대해 두 클래스 간의 마진을 최대화하는 결정 경계를 찾아내며, 이는 복잡한 분류 문제에 대해 높은 성능을 발휘할 수 있게 해줍니다.
3.8 Training SVM

3.9 Example – linear SVM

3.10 Linear SVM – Test phase
Linear SVM – 테스트 단계 테스트 단계에서는 결정 경계의 매개변수를 찾은 후, 테스트 인스턴스 z가 다음과 같이 분류됩니다. 결정 경계의 매개변수 (w)와 (b)가 학습 단계에서 찾아진 후, 테스트 단계에서는 이 매개변수들을 사용하여 새로운 테스트 인스턴스 (z)가 어느 클래스에 속하는지를 결정합니다. 이를 위해 다음과 같은 결정 함수를 사용합니다. [ f(z) = w \cdot z + b ] 여기서, (w)는 결정 경계의 방향을 나타내는 벡터이고, (b)는 결정 경계의 위치를 조정하는 스칼라 값입니다. 이 함수의 결과값이 양수이면 테스트 인스턴스 (z)를 하나의 클래스로 분류하고, 음수이면 다른 클래스로 분류합니다. 결과적으로, 이러한 방식으로 SVM 모델은 새로운 테스트 데이터에 대해 분류를 수행할 수 있습니다.

3.11 Practice problem: Linear SVM
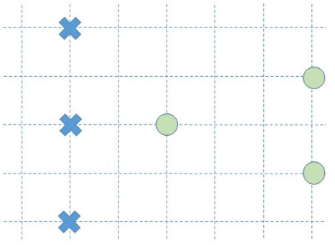
• Decision boundary • Support vectors • Training error
3.12 Linear SVM: non-separable case
- 선형 SVM은 문제가 선형적으로 분리가능하지 않은 경우, 즉 실제 데이터가 잡음이 많고 거의 결코 선형적으로 분리될 수 없는 경우에도 사용할 수 있습니다.
- 이러한 상황에서는 '소프트 마진 접근법'을 사용합니다.
- 소프트 마진 접근법은 약간의 오류를 허용하면서 최대 마진을 찾는 방식입니다.
- 이는 모든 데이터 샘플이 완벽하게 분류될 필요가 없다는 것을 의미하며, 일부 데이터 샘플은 잘못 분류될 수 있습니다.
- 이를 위해 소프트 마진 SVM은 슬랙 변수(slack variables, ξ)를 도입하여 각 데이터 포인트가 마진 내부에 있거나 심지어 잘못 분류되는 것을 허용합니다.
- 목표는 다음과 같은 새로운 최적화 문제를 해결하는 것입니다: 1/2 ||w||^2 + C Σξ_i를 최소화합니다.
- 여기서 C는 오류에 대한 페널티를 결정하는 매개변수입니다.
- C 값이 크면 오류에 대한 페널티가 커지고, 모델은 훈련 데이터에 더 잘 맞으려고 하지만 오버피팅의 위험이 있습니다.
- 반면, C 값이 작으면 오류에 대한 페널티가 줄어들고 모델은 더 유연해지지만 언더피팅될 수 있습니다.
- 이러한 방식으로, 소프트 마진 SVM은 선형적으로 분리가능하지 않은 데이터에 대해서도 효과적으로 작동할 수 있으며, 실제 세계의 복잡한 데이터셋에서 유용하게 사용됩니다.

3.13 Slack variables for non-separable data

3.14 Linear SVM: non-separable case

- 선형 SVM에서 데이터가 선형적으로 분리 가능하지 않은 경우, 이 문제를 해결하기 위해 '슬랙 변수(slack variables)'와 'C'라는 조정 파라미터를 도입합니다.
- 슬랙 변수 (Slack Variables) 슬랙 변수는 데이터 포인트가 마진 내부에 있거나 심지어 잘못 분류될 수 있도록 허용하는 변수입니다.
- 이를 통해 모델이 완벽하게 분리 가능하지 않은 데이터에 대해서도 적용될 수 있습니다.
- 각 데이터 포인트에 대해 슬랙 변수를 도입함으로써, 일부 데이터 포인트가 결정 경계의 잘못된 쪽에 위치할 수 있으며, 이는 더 유연한 결정 경계를 만듭니다.
- C: 조정 파라미터 (Tuning Parameter) 'C' 파라미터는 소프트 마진의 정도를 결정하는 조정 파라미터(규제 파라미터)입니다.
- 이는 오분류를 얼마나 용납할 것인지를 결정하는데, C 값이 크면 오분류에 대한 패널티가 커져서 마진이 좁아지지만, 오분류를 줄일 수 있습니다.
- 반면, C 값이 작으면 오분류에 대한 패널티가 작아져서 마진이 넓어지지만, 일부 오분류를 허용하게 됩니다.
- 즉, C 값을 조정함으로써 모델의 일반화 성능을 조절할 수 있습니다. 이러한 방식으로, 선형 SVM은 선형적으로 분리 가능하지 않은 복잡한 데이터셋에 대해서도 유연하게 적용될 수 있으며, 슬랙 변수와 C 파라미터를 통해 모델의 오차 허용도와 규제의 정도를 조절할 수 있습니다.
3.15 Regularization parameter

3.16 Linear SVM - summary
- 선형 SVM 요약: 훈련 단계 선형 SVM에서의 훈련 단계는 결정 경계(파라미터 w와 b)를 얻기 위해 제약이 있는 최적화 문제를 해결하는 과정을 포함합니다.
- 분리 가능한 경우: 최대 마진(하드 마진)을 사용합니다.
- 이는 데이터를 완벽하게 분류하는 결정 경계를 찾으려고 시도하는 것으로, 두 클래스 사이의 마진을 최대화하는 파라미터 w와 b를 찾습니다. 분리 불가능한 경우: 소프트 마진 접근 방식을 사용합니다.
- 실제 데이터는 잡음이 있고 거의 결코 선형적으로 분리될 수 없기 때문에, 일부 데이터 포인트가 잘못 분류될 수 있도록 허용하면서도 마진을 최대한 크게 하려고 합니다.
- 이를 위해 슬랙 변수를 도입하고, C라는 조정 파라미터(정규화 파라미터)를 사용하여 소프트 마진을 구현합니다.
- 테스트 단계 훈련 단계에서 결정된 결정 경계의 파라미터 w와 b를 바탕으로, 새로운 데이터 포인트(테스트 인스턴스)가 주어졌을 때 이를 분류합니다.
- 새로운 데이터 포인트 z에 대하여, 결정 함수 f(z) = w * z + b를 사용하여 분류를 수행합니다.
- 이 함수의 결과가 양수인 경우 한 클래스로, 음수인 경우 다른 클래스로 분류됩니다.
- 이와 같이, 선형 SVM은 훈련 단계에서 최적의 결정 경계를 찾아내고, 테스트 단계에서는 이 결정 경계를 사용하여 새로운 데이터 포인트의 분류를 수행합니다.

3.17 Problems with linear SVM




