Outline
Bias-variance tradeoff &Cross-validation- Performance metrics for classification
HYPERPARAMETER TUNING THROUGH CROSS VALIDATION
2.1 Learning curves for hyperparameter tuning
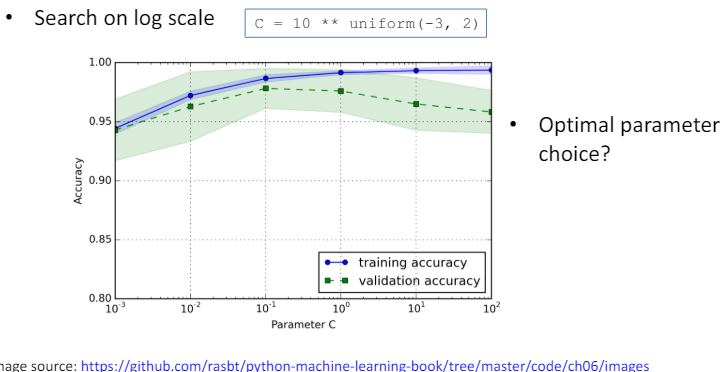
- 하이퍼파라미터 튜닝에 있어서 학습 곡선을 활용하는 것은 매우 중요합니다.
- 학습 곡선은 모델이 훈련 데이터와 검증 데이터에 대해 어떻게 수행하는지를 시각적으로 보여주며, 이를 통해 모델의 과적합(overfitting) 또는 과소적합(underfitting) 여부를 판단할 수 있습니다.
- 하이퍼파라미터를 조정할 때, 최적의 선택을 찾기 위해서는 몇 가지 중요한 점을 고려해야 합니다.
- 최적의 파라미터 선택: 모델의 학습 곡선을 분석하여, 훈련 데이터와 검증 데이터에 대한 성능 차이가 최소화되면서도, 전체적인 성능이 우수한 하이퍼파라미터 값을 찾아야 합니다.
- 이 과정에서 과적합과 과소적합의 균형을 잘 맞추는 것이 중요합니다.
- 로그 스케일에서의 탐색: 하이퍼파라미터 값의 범위가 넓거나, 소수의 변화에도 모델 성능에 큰 영향을 미칠 때는 로그 스케일에서의 탐색을 고려해야 합니다.
- 예를 들어, 학습률(learning rate)과 같은 하이퍼파라미터는 로그 스케일에서 탐색하는 것이 효과적입니다.
- 로그 스케일 탐색을 통해 보다 넓은 범위의 값들을 효율적으로 탐색하고, 최적값을 더 정밀하게 찾아낼 수 있습니다.
- 학습 곡선과 로그 스케일 탐색을 통한 하이퍼파라미터 튜닝은 모델의 성능을 최적화하는 데 있어 필수적인 과정입니다.
- 이를 통해 데이터에 가장 잘 맞는 모델을 구성하고, 최종적으로 더 높은 예측 성능을 달성할 수 있습니다.
2.2 Grid search
- 그리드 서치(Grid Search)는 하이퍼파라미터를 조정하기 위한 완전 탐색(brute-force exhaustive search) 방법입니다.
- 이 방법에서는 다양한 값들의 목록을 지정하고, 각 조합에 대한 모델 성능을 평가합니다.
- 하이퍼파라미터 값 목록 설정: 우선, 조정하고자 하는 하이퍼파라미터들에 대한 가능한 값들의 목록을 설정합니다.
- 예를 들어, 결정 트리의 깊이(depth), SVM의 C 값 등이 이에 해당할 수 있습니다.
- 조합의 평가: 설정한 목록에 기반하여 가능한 모든 하이퍼파라미터 조합을 생성하고, 각 조합에 대해 모델을 훈련시킨 후 성능을 평가합니다.
- 이 과정에서 보통 교차 검증(cross-validation)을 사용하여 각 조합의 성능을 평가합니다.
- 최적의 조합 선택: 모든 조합에 대한 성능 평가가 끝나면, 가장 좋은 성능을 보인 하이퍼파라미터 조합을 선택합니다.
- 그리드 서치는 매우 직관적이고 간단한 방법입니다.
- 그러나 가능한 모든 조합을 평가해야 하기 때문에, 하이퍼파라미터의 개수가 많거나 각 하이퍼파라미터의 가능한 값의 범위가 크면 계산 비용이 매우 커질 수 있습니다.
- 이러한 경우에는 랜덤 서치(Random Search)나 베이지안 최적화(Bayesian Optimization)와 같은 다른 탐색 방법을 고려할 수 있습니다.
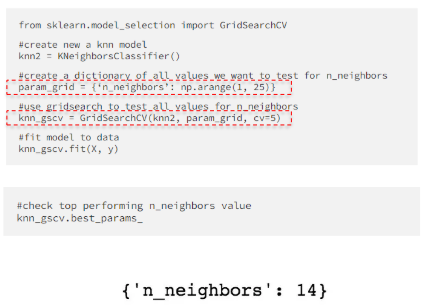
- Grid search 방법에서 하나 이상의 하이퍼파라미터가 있을 때, 모델 학습이 수행되는 횟수는 모든 하이퍼파라미터의 가능한 값 조합의 총 개수에 의해 결정됩니다.
- 예를 들어, 두 개의 하이퍼파라미터가 있고, 첫 번째 하이퍼파라미터에 대해 4개의 다른 값을 고려하고, 두 번째 하이퍼파라미터에 대해 3개의 다른 값을 고려한다고 가정합시다.
- 이 경우, 가능한 모든 조합은 4 x 3 = 12개입니다.
- 따라서, 이 예에서 모델 학습은 총 12번 수행됩니다.
- 전반적으로, 만약 (n)개의 하이퍼파라미터가 있고, 각각 (k_1, k_2, ..., k_n)개의 가능한 값을 가진다면, 총 모델 학습 횟수는 (k_1 \times k_2 \times ... \times k_n)이 됩니다.
- 이 방법은 가능한 모든 조합을 탐색하기 때문에 모델의 최적 하이퍼파라미터 조합을 찾을 수 있는 장점이 있지만, 많은 시간과 계산 자원을 요구할 수 있습니다.

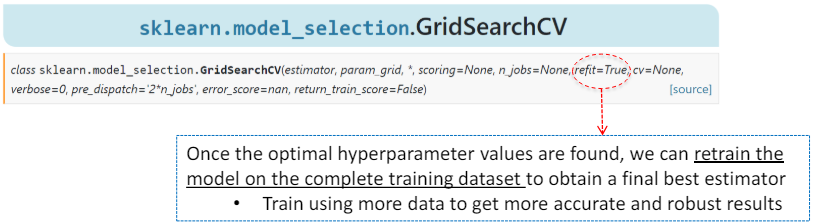
- 최적의 하이퍼파라미터 값을 찾은 후에는, 완전한 훈련 데이터셋을 사용하여 모델을 다시 훈련시켜 최종적으로 최적의 추정기를 얻을 수 있습니다.
- 더 많은 데이터를 사용하여 훈련시키면 결과가 더 정확하고 강건해집니다.
- 이렇게 재훈련된 추정기는 best_estimator_ 속성에서 사용할 수 있게 되며, 이 GridSearchCV 인스턴스를 직접 사용하여 predict 함수를 호출할 수 있게 해줍니다.
- 이러한 접근 방식은 최적화된 하이퍼파라미터를 기반으로 모델의 성능을 최대화하려는 경우에 유용합니다.
- 특히, GridSearchCV를 사용하여 광범위한 하이퍼파라미터 공간을 탐색하고 최적의 조합을 찾은 후, 이 최적의 조합으로 모델을 전체 훈련 데이터셋에 대해 다시 훈련시키면, 보다 일반화된 모델을 얻을 수 있습니다.
- 이는 모델이 새로운, 보지 못한 데이터에 대해 더욱 잘 일반화될 수 있게 해줍니다.
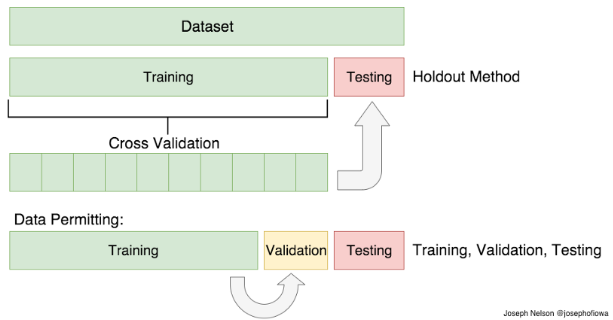
2.3 Recall: Train/Validation/Test set
2.4 Randomized search
- Randomized Search는 지정된 분포에서 매개변수 설정을 샘플링하는 방법입니다.
- 이 방법에서는 사전에 정의된 고정된 수의 매개변수 설정(n_iter)을 샘플링하여 모델의 성능을 평가합니다. 매개변수 분포 지정: 사용자는 각 매개변수에 대해 연속적인 분포나 이산적인 분포를 지정합니다.
- 예를 들어, 결정 트리의 깊이에 대해 균일 분포를 지정할 수 있으며, SVM의 C 매개변수에 대해 로그 균일 분포를 지정할 수 있습니다.
- 샘플링을 통한 매개변수 설정 선택: 지정된 분포에서 무작위로 n_iter 횟수만큼 매개변수 설정을 샘플링하여 선택합니다.
- 이 방법은 그리드 서치와 달리 모든 가능한 조합을 탐색하지 않고, 고정된 수의 조합만을 탐색합니다.
- 모델 성능 평가: 선택된 각 매개변수 설정에 대해 모델을 훈련시키고 성능을 평가합니다. 일반적으로 교차 검증을 사용하여 각 설정의 성능을 평가합니다.
- Randomized Search는 매개변수 공간의 크기에 상관없이 사용자가 지정한 n_iter의 수만큼만 평가를 수행하기 때문에, 그리드 서치보다 계산 비용이 훨씬 낮은 경우가 많습니다.
- 또한, 매개변수 공간 전체를 탐색하지 않기 때문에 그리드 서치에 비해 덜 철저할 수 있지만, 대규모 매개변수 공간에서 빠르게 좋은 매개변수 조합을 찾는 데 효과적입니다.

PERFORMANCE MEASURE
2.5 Performance measure
성능 측정은 테스트 데이터 X에 대해, 실제 레이블 Ytrue와 예측된 레이블 Ypred 사이의 근접성을 측정하는 것을 의미합니다. 여기서 중요한 것은 분류기를 학습하거나 분류하는 속도, 확장성 등이 아니라 예측의 정확도입니다. 성능 측정의 한 방법으로 혼동 행렬(Confusion Matrix)이 자주 사용됩니다. 혼동 행렬은 실제 레이블과 모델이 예측한 레이블을 비교하여, 모델의 성능을 이해할 수 있는 표입니다. 이 행렬은 다음과 같은 네 가지 기본 요소로 구성됩니다: True Positive (TP): 실제 양성 클래스를 양성으로 올바르게 분류한 경우의 수 False Positive (FP): 실제는 음성 클래스이지만, 양성으로 잘못 분류한 경우의 수 True Negative (TN): 실제 음성 클래스를 음성으로 올바르게 분류한 경우의 수 False Negative (FN): 실제는 양성 클래스이지만, 음성으로 잘못 분류한 경우의 수 혼동 행렬을 통해, 정밀도(Precision), 재현율(Recall), F1 점수 같은 다양한 성능 지표를 계산할 수 있으며, 이를 통해 모델의 성능을 정량적으로 평가할 수 있습니다. 이러한 지표들은 모델이 데이터를 얼마나 잘 분류하는지, 특히 양성 클래스를 얼마나 잘 감지하는지 등을 이해하는 데 도움을 줍니다.

2.6 Confusion matrix
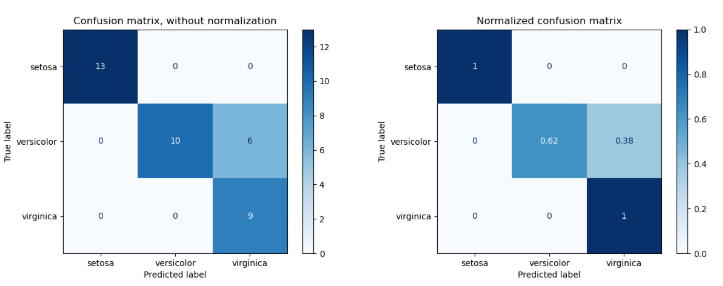
2.7 Example
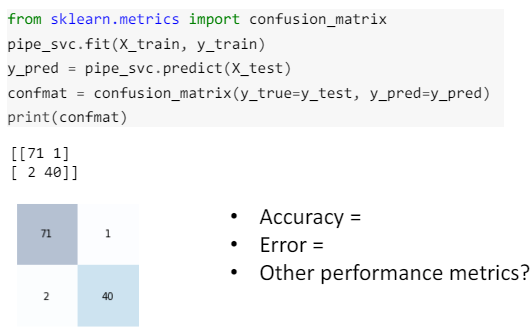
2.8 Example: MNIST handwritten digits

2.9 Binary Classification
2.10 Performance metrics
분류 알고리즘의 진정한 성능을 나타내기 위해서는 정확도(또는 오류)만으로는 부족할 수 있습니다. 이를 보완하기 위해 다음과 같은 성능 지표들이 사용됩니다: 민감도/특이도(Sensitivity/Specificity): 민감도는 실제 양성을 양성으로 올바르게 예측한 비율을, 특이도는 실제 음성을 음성으로 올바르게 예측한 비율을 나타냅니다. 정밀도/재현율(Precision/Recall), F1 점수: 정밀도는 양성으로 예측된 경우 중 실제로 양성인 비율을, 재현율은 실제 양성 중 양성으로 올바르게 예측된 비율을 나타냅니다. F1 점수는 정밀도와 재현율의 조화 평균을 통해 두 지표의 균형을 평가하는 지표입니다. ROC 곡선, AUC(Area Under the Curve): ROC 곡선은 민감도(재현율)와 1-특이도(거짓 양성 비율) 사이의 관계를 그래프로 나타내며, AUC는 ROC 곡선 아래의 면적으로, 분류기의 성능을 하나의 숫자로 요약합니다. AUC 값이 1에 가까울수록 성능이 우수함을 나타냅니다. 이러한 성능 지표들은 분류 모델의 다양한 측면을 평가하고, 특히 불균형 데이터셋에서 모델의 성능을 보다 정확하게 이해하는 데 도움이 됩니다.
SENSITIVITY & SPECIFICITY
2.11 Performance measure
성능 측정에서 관심 있는 클래스를 '양성 클래스'라고 하며, 나머지 모든 클래스는 '음성'으로 분류됩니다. 이러한 분류에서 다음과 같은 용어들을 사용합니다: True Positive (TP, 진양성): 관심 클래스로 올바르게 분류된 경우입니다. False Negative (FN, 가음성): 관심 클래스가 아니라고 잘못 분류된 경우입니다. False Positive (FP, 가양성): 관심 클래스로 잘못 분류된 경우입니다. True Negative (TN, 진음성): 관심 클래스가 아닌 것으로 올바르게 분류된 경우입니다. 이러한 개념들은 분류 모델의 성능을 평가하고 이해하는 데 필수적입니다.
2.12 Accuracy
2.13 Limitation of Accuracy
이진 분류에서 정확도의 한계를 이해하기 위해 다음과 같은 상황을 고려해 보겠습니다: 클래스 0의 예시가 9990개 있고, 클래스 1의 예시가 단 10개 있다고 가정해 봅시다. 분류기가 모든 예시를 클래스 0으로 예측한다면, 정확도는 매우 높게 나올 것입니다. 그러나 이 경우 정확도는 오해의 소지가 있습니다. 왜냐하면 분류기가 단 한 개의 클래스 1 예시도 감지하지 못했기 때문입니다. 이러한 상황에서는 클래스 1 예시가 극히 드물기 때문에, 심지어 모든 예시를 클래스 0으로 잘못 분류해도 높은 정확도를 얻을 수 있습니다. 이는 정확도만을 성능 지표로 사용할 때의 주요 한계점 중 하나입니다. 특히 불균형한 데이터 세트에서는 이러한 문제가 더욱 심각해집니다. 따라서 이러한 경우 정확도 외에도 다른 성능 지표들(예: 정밀도, 재현율, F1 점수)을 함께 고려하는 것이 중요합니다.
2.14 Sensitivity & Specificity
2.15 Example

