Content
Introduction to supervised learning approachData split in supervised learning- Classification algorithms
KNN & distance measuresDecision treeRandom Forest, Ensemble approach- SVM
3. Classification algorithms - SVM( SUPPORT VECTOR MACHINE )
SVM: Content
1. Linear SVM
2. Linear SVM: non-separable case
3. Non-linear SVM – Kernel trick
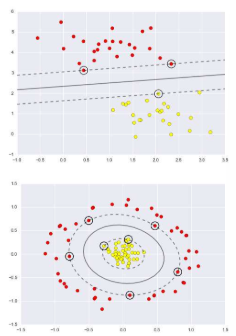
3.18 Non-linear SVMs
선형으로 분리 가능한 데이터셋에 약간의 잡음이 있을 때, 선형 SVM은 훌륭한 결과를 제공합니다. 그러나 데이터셋이 너무 복잡하여 선형으로 분리가 어려운 경우는 어떻게 해야 할까요? 이러한 상황에서는 데이터를 더 높은 차원의 공간으로 매핑하는 방법을 고려할 수 있습니다. 더 높은 차원으로 데이터를 매핑하면, 원래의 데이터 공간에서는 선형으로 분리가 불가능했던 데이터들이 새로운 고차원 공간에서는 선형으로 분리가 가능해질 수 있습니다. 이런 방식은 비선형 SVM에서 주로 사용되며, 이 과정에서 커널 트릭(Kernel Trick)이라는 기법을 활용합니다. 커널 트릭을 사용하면 실제로 데이터를 고차원으로 변환하지 않고도 고차원에서의 내적을 계산할 수 있어, 계산 비용을 크게 절감할 수 있습니다. 이를 통해 복잡하고 비선형적인 데이터셋에 대해서도 효과적으로 분류 경계를 찾을 수 있게 됩니다.

3.19 Nonlinear SVM
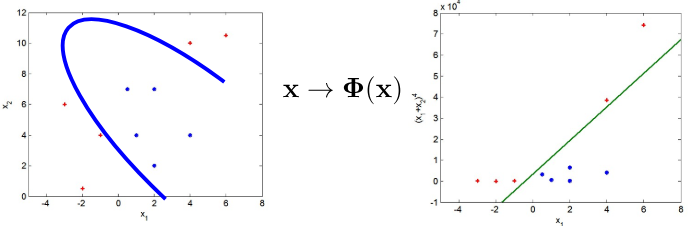
- 비선형 SVM에 대해 설명하자면, 결정 경계가 선형이 아닐 경우 어떻게 해야 할까요?
- 이런 상황에서는 데이터를 새로운 공간으로 변환하여, 그 공간에서는 선형 경계를 사용해 인스턴스를 분리할 수 있게 합니다. 비선형 문제를 해결하기 위해 데이터를 더 높은 차원의 공간으로 매핑하는 기법을 사용합니다.
- 이렇게 하면 원래의 공간에서는 선형으로 분리가 불가능했던 데이터도 새로운 공간에서는 선형 분리가 가능해질 수 있습니다.
- 이 과정에서 핵심적인 역할을 하는 것이 바로 커널 트릭(Kernel Trick)입니다.
- 커널 트릭을 사용하면 실제로 데이터를 높은 차원으로 변환하지 않고도, 그러한 변환을 한 것과 동일한 효과를 얻어 계산 비용을 크게 절감할 수 있습니다. 결국, 비선형 SVM은 복잡한 비선형 데이터에 대해서도 효과적으로 분류할 수 있는 강력한 방법을 제공합니다.
3.20 SVM with polynomial kernel visualization

3.21 Extension to Non-linear Decision Boundary
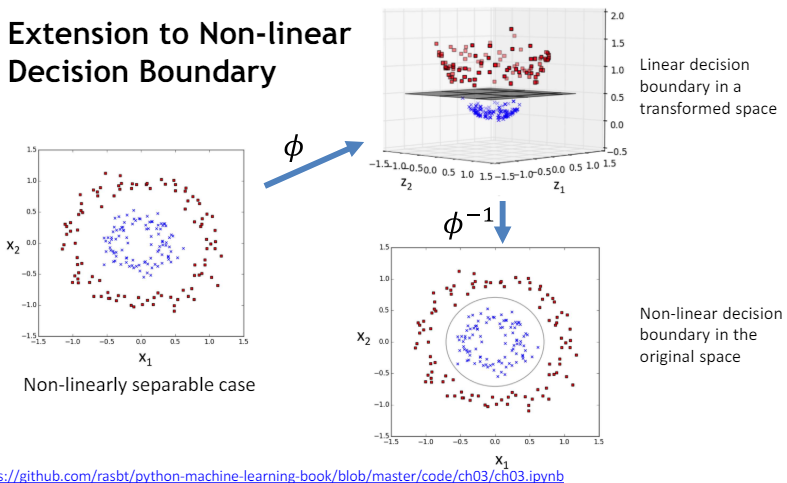
3.22 Learning nonlinear SVM

3.23 Issues in nonlinear SVM
- 비선형 SVM에서는 두 가지 주요 문제점이 있습니다.
- 매핑 함수 찾기: 비선형 데이터를 처리하기 위해, 데이터를 더 높은 차원의 공간으로 매핑하는 함수를 찾아야 합니다.
- 그러나 이 매핑 함수를 직접 찾는 것은 매우 어려울 수 있습니다.
- 고차원 공간에서의 계산 비용: 데이터를 고차원 공간으로 매핑하면, 그 공간에서의 계산이 매우 비싸질 수 있습니다. 이는 고차원에서의 벡터 계산이 많은 컴퓨터 자원을 요구하기 때문입니다. 이러한 문제들을 해결하기 위해 커널 트릭을 사용합니다.
- 커널 트릭은 고차원 공간으로의 데이터 매핑 없이, 직접적인 계산을 통해 고차원에서의 내적을 효율적으로 계산할 수 있게 해 줍니다. 이 방법을 통해, 비선형 SVM에서의 계산 비용을 크게 줄이면서도 고차원의 특성 공간에서의 판별 경계를 효과적으로 찾을 수 있습니다. 따라서 커널 트릭은 비선형 SVM에서 매우 중요한 역할을 합니다.
3.24 Kernel function
커널 함수는 고차원 공간에서의 점곱을 원래 공간에서의 유사도로 표현할 수 있게 해주는 함수입니다. 즉, 어떤 커널 함수 (K)가 존재하여, 변환된 공간에서의 점곱(dot product)을 원본 공간에서의 유사도(similarity) 관점으로 표현할 수 있습니다. 이는 고차원으로 데이터를 실제로 변환하지 않고도, 고차원에서의 점곱 연산을 효율적으로 수행할 수 있게 해주는 핵심 아이디어입니다. 예를 들어, 선형이 아닌 데이터를 선형으로 분리 가능하게 만들기 위해 데이터를 더 높은 차원으로 매핑하는 과정에서, 실제로 데이터를 변환하는 대신 커널 함수를 사용합니다. 이 커널 함수는 원본 데이터의 두 샘플 간의 유사도를 고차원 공간에서의 점곱으로 해석해 줍니다. 가장 널리 사용되는 커널 함수로는 선형 커널, 다항식 커널, RBF(가우시안) 커널 등이 있습니다. 이 방법을 통해, SVM과 같은 알고리즘이 복잡한 비선형 문제를 효과적으로 해결할 수 있게 됩니다.

3.25 Examples of Kernel Functions

3.26 Kernel Trick
- 커널 트릭은 고차원 공간에서의 데이터를 처리할 때 매우 중요한 기법입니다.
- 이 기법의 핵심은 다음과 같습니다:
- K: 커널 함수 - 커널 함수는 두 입력 벡터 간의 내적을 고차원 공간에서 표현할 수 있게 해줍니다.
- 내적 계산의 효율성 - 고차원 공간으로의 데이터 변환 후 내적을 계산하는 것보다 커널 함수를 사용하여 내적을 계산하는 것이 훨씬 더 효율적입니다.
- 변환 함수 Φ의 명시적인 지식 불필요 - 커널 트릭의 가장 큰 장점 중 하나는 고차원으로의 매핑 함수 Φ의 정확한 형태를 명시적으로 알 필요가 없다는 것입니다.
- 커널 함수를 통해 직접적으로 고차원 공간에서의 내적 결과를 얻을 수 있기 때문입니다.
- 이러한 특징 덕분에, 커널 트릭은 SVM을 비롯한 여러 머신러닝 알고리즘에서 복잡한 비선형 문제를 해결하는 데 큰 도움을 줍니다.
- 사용자는 적절한 커널 함수를 선택하기만 하면, 알고리즘이 고차원 공간에서의 복잡한 패턴을 효율적으로 학습할 수 있게 됩니다.
3.27 Example transformation

3.28 Example – Linear vs. RBF kernel

3.29 Non-linear SVM: test phase

비선형 SVM에서 테스트 단계의 결정 함수는 다음과 같이 주어집니다: [f(x) = \sum_{i=1}^{m} \lambda_i y_i K(x_i, x) + b] 여기서 (m)은 서포트 벡터의 수, (\lambda_i)는 각 서포트 벡터에 대응하는 라그랑주 승수, (K(x_i, x))는 테스트 샘플과 각 서포트 벡터 (x_i) 사이의 유사성을 평가하는 커널 함수입니다. 만약 (f(x) > 0)이면 (y=1)이 됩니다. 그렇지 않으면 (y=-1)입니다. 테스트 단계의 시간 복잡도는 서포트 벡터의 수에 의존합니다. 즉, 서포트 벡터의 수가 많을수록 테스트 단계에서 더 많은 계산이 필요하게 됩니다. 이러한 이유로, 비선형 SVM에서는 서포트 벡터의 수를 최소화하는 것이 중요합니다. 서포트 벡터는 결정 경계 근처에 위치한 데이터 포인트들로, 분류 결정에 중요한 역할을 합니다. 커널 함수는 이러한 서포트 벡터와 테스트 샘플 간의 유사도를 계산하여, 새로운 샘플이 어느 카테고리에 속하는지 결정하는 데 사용됩니다.
3.30 Complexity
- SVM의 계산 및 저장 요구 사항은 훈련 샘플의 수가 증가함에 따라 급격히 증가합니다. 특히 비선형 SVM에서 커널 트릭을 사용할 경우에는 그 복잡성이 더욱 커집니다.
- 비선형 SVM과 커널 트릭: 커널 트릭을 사용하는 비선형 SVM의 경우, 계산 복잡도는 일반적으로 이차 계획법(QP, Quadratic Programming) 솔버에 대해 (O(n^2))에서 (O(n^3)) 사이입니다.
- 여기서 (n)은 훈련 샘플의 수입니다. 공간 복잡도: 커널 행렬을 저장하는데 (O(n^2))의 공간이 필요합니다.
- 이는 모든 훈련 샘플 간의 커널 계산 결과를 저장해야 하기 때문입니다. 선형 SVM: 선형 SVM의 경우, 효율적인 구현(예: 확률적 경사 하강법을 사용하는 경우)은 보통 더 낮은 복잡성을 가집니다.
- 그러나 구체적인 복잡성은 구현 방법, 사용된 커널, 그리고 데이터셋에 크게 의존합니다.
- 결론적으로, SVM의 계산 및 저장 복잡도는 모델의 유형(선형 또는 비선형), 사용된 커널의 종류, 구현 방식, 그리고 처리해야 하는 데이터셋의 특성에 따라 크게 달라질 수 있습니다. 따라서 효율적인 SVM 모델을 생성하고 사용하기 위해서는 이러한 요소들을 고려하여 최적화하는 것이 중요합니다.
3.31 SVM summary
- SVM(Support Vector Machine)은 효율적인 알고리즘이 가능한 제약된 볼록 최적화 문제입니다.
- 이의 주요 요소는 다음과 같습니다:
- 결정 경계의 마진 최대화: SVM은 클래스 간의 결정 경계를 정의하며, 이 경계와 가장 가까운 훈련 샘플들 사이의 마진을 최대화하는 방향으로 모델을 학습합니다.
- 이를 통해 일반화 능력이 향상됩니다. 커널 트릭: 비선형 데이터에 대해서도 잘 작동하도록 하기 위해 도입된 기법입니다. 커널 트릭을 사용하면 고차원 공간에서 데이터를 더 쉽게 분류할 수 있게 됩니다.
- 하이퍼파라미터: 사용자는 커널 함수의 유형과 슬랙 변수를 위한 비용 함수 C와 같은 하이퍼파라미터를 제공해야 합니다. 이러한 하이퍼파라미터는 모델의 성능에 중요한 영향을 미칩니다.
- 다중 클래스 문제로의 확장: 기본적으로 SVM은 이진 분류 문제에 사용되지만, 다중 클래스 분류 문제에도 확장될 수 있으며, 이를 위해 여러 방법들이 개발되었습니다.
- 요약하자면, SVM은 결정 경계의 마진을 최대화하여 고차원 공간에서도 효과적으로 데이터를 분류할 수 있는 강력한 기계 학습 모델입니다.
- 하지만, 최적의 성능을 얻기 위해서는 적절한 하이퍼파라미터 선택이 필수적입니다.



