Content
Introduction to supervised learning approachData split in supervised learning- Classification algorithms
KNN & distance measuresDecision tree- Random Forest, Ensemble approach
SVM
3. Classification algorithms - Random Forest, Ensemble approach
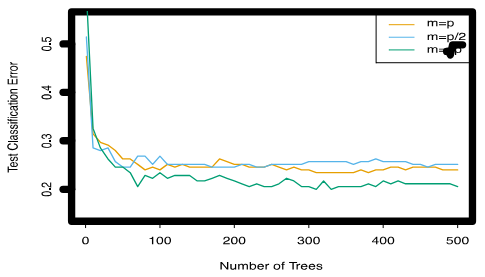
3.17 Random Forest with different values of “m”
Random Forest 알고리즘에서 다양한 "m" 값의 사용은 중요한 의미를 가집니다. 여기서 "m"은 각 결정 트리를 생성할 때 무작위로 선택되는 특성(변수)의 수를 의미합니다. "p"는 사용 가능한 전체 특성의 수입니다. 만약 Random Forest를 구축할 때 "m=p"로 설정한다면, 이는 단순히 Bagging과 동일한 방법이 됩니다. 즉, 각 트리를 만들 때 모든 특성을 사용하는 것이므로 무작위 특성 선택의 과정이 사라지게 됩니다. 이 경우, 각 트리는 더 유사해질 가능성이 높고, 따라서 Bagging에서 언급된 문제점인 높은 상관관계로 인한 분산 감소 효과의 한계를 경험할 수 있습니다. 반면에, "m"을 "p"보다 작게 설정하면, 각 트리는 무작위로 선택된 특성들을 기반으로 구축되므로 서로 다른 특성 조합을 학습하게 됩니다. 이는 트리 간의 상관관계를 줄이고 전체 모델의 다양성을 증가시키며, 결과적으로 더 나은 분산 감소 효과와 예측 성능을 달성할 수 있습니다. 따라서 "m"의 값은 Random Forest 모델의 성능에 중요한 영향을 미치며, 적절한 "m" 값을 선택하는 것은 모델의 정확도와 안정성을 최적화하는 데 핵심적인 요소입니다.
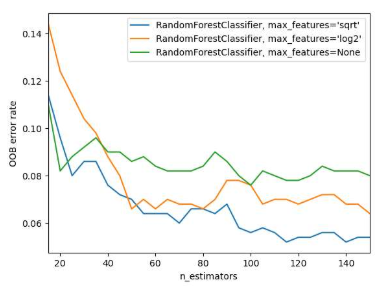
3.18 Out-of-bag (OOB) error
- Out-of-bag (OOB) 오류는 랜덤 포레스트 모델을 검증하는 방법 중 하나입니다.
- 랜덤 포레스트는 부트스트랩 샘플링(복원 추출)을 통해 각 트리를 생성하는데, 이 과정에서 일부 샘플은 어떤 트리에서도 사용되지 않을 수 있습니다.
- 이러한 샘플들을 OOB(Out-of-bag) 샘플이라고 합니다.
- OOB 오류는 OOB 샘플에 대한 모델의 예측 오류를 계산함으로써 얻어집니다.
- 구체적으로, 각 OOB 샘플에 대해 해당 샘플을 생성하는데 사용되지 않은 트리들만을 사용하여 예측을 수행하고, 이 예측값들과 실제 값 사이의 차이를 평가합니다.
- 이렇게 계산된 OOB 오류는 별도의 검증 데이터 세트 없이도 모델의 일반화 성능을 평가할 수 있게 해줍니다.
- 일반적으로 OOB 오류는 교차 검증을 통해 얻은 오류와 유사한 경향을 보여줍니다.
- 따라서, OOB 오류는 랜덤 포레스트 모델을 튜닝하고 검증하는 데 유용한 도구로 사용됩니다.
3.19 Variable Importance Measure
- 변수 중요도 측정:
- 배깅(Bagging)은 일반적으로 단일 트리를 사용하는 것보다 예측 정확도를 향상시키지만, 모델을 해석하기 어렵게 만듬.
- 수백 개의 트리가 있을 때 어떤 변수들이 절차에 가장 중요한지 명확하지 않음.
- 따라서, 배깅은 해석 가능성을 희생하면서 예측 정확도를 개선.
- 그러나, 상대적 영향도(Relative Influence) 플롯을 사용하여 각 예측 변수의 중요도에 대한 전반적인 요약을 여전히 얻을 수 있다.
- 상대적 영향도 플롯은 모델의 예측에 각 변수가 얼마나 영향을 미치는지 비교.
- 이는 각 변수가 분할에 사용될 때 성능 지표(예: 불순도 감소)에 평균적으로 얼마나 기여하는지 측정함으로써 계산됩니다.
- 결과적으로, 이러한 그래프는 많은 트리로 구성된 복잡한 모델에서도 어떤 변수들이 가장 중요한지 이해하는 데 도움을 줍니다.
3.20 Relative Influence Plots
상대적 영향력 도표(relative influence plots)는 어떤 변수가 응답을 예측하는 데 가장 유용한지 결정하는 데 도움을 줍니다. 이 도표는 각 변수에 대한 점수를 제공합니다. 점수가 0에 가까울수록 해당 변수는 중요하지 않다는 것을 의미하며, 제거될 수 있습니다. 점수가 클수록 변수가 가지는 영향력이 더 크다는 것을 나타냅니다. 예를 들어, 변수에 의해 가져온 지니 불순도(Gini impurity)의 (정규화된) 총 감소량이나 평균 제곱 오차(MSE)의 감소량 등이 이에 해당됩니다. 이러한 방식으로, 상대적 영향력 도표는 모델에서 각 변수의 중요성을 비교할 수 있는 효과적인 방법을 제공하며, 이는 결정 트리 기반의 앙상블 모델인 랜덤 포레스트나 부스팅 모델 등에서 변수의 중요도를 평가하는 데 유용하게 사용됩니다. 따라서, 이 도표를 통해 어떤 변수가 예측에 중요한 역할을 하는지, 어떤 변수가 불필요한지를 파악할 수 있어 모델의 성능을 향상시키고 해석을 용이하게 하는 데 도움을 줄 수 있습니다.
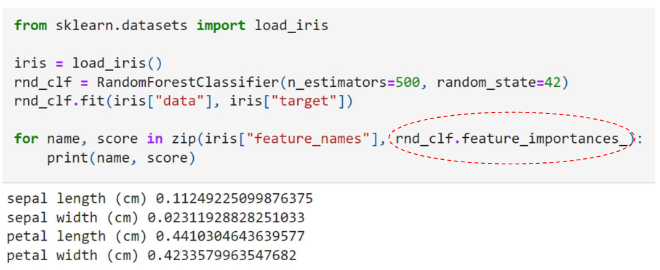
3.21 Example: Iris data
3.22 Example: Housing Data
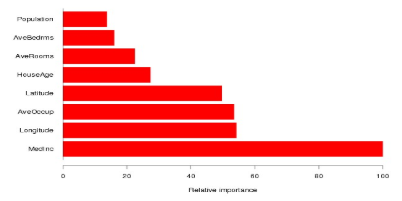
예시: 주택 데이터 분석에서 중간 소득이 가장 중요한 변수로 나타났습니다. 경도, 위도 및 평균 거주율이 그 다음으로 중요한 변수로 확인되었습니다. 이러한 결과는 주택 가격이나 주택 시장의 특성을 예측하는 데 있어서, 중간 소득이 매우 결정적인 요소임을 보여주며, 위치와 거주 밀도 또한 중요한 영향을 미치는 것으로 나타납니다.
3.23 Boosting approach
부스팅 접근 방법은 성능이 약한 분류기(예: 간단한 결정 트리) 여러 개를 선형으로 연결하여 강한 성능의 학습기를 만드는 앙상블 기술입니다. 이 방식은 순차적으로, 이전 학습기의 결과를 바탕으로 성능을 조금씩 향상시켜 나갑니다. 처음에 샘플링한 데이터 세트를 분류하고 잘못 분류된 데이터에 더 큰 가중치를 부여하여 다시 샘플링하는 방식으로 작동합니다. 부스팅의 대표적인 예로는 AdaBoost와 그래디언트 부스팅(Gradient Boost)이 있습니다. AdaBoost: AdaBoost는 잘못 분류된 데이터 포인트에 더 많은 가중치를 부여하면서 여러 개의 약한 학습기를 순차적으로 학습시킵니다. 각 단계에서 AdaBoost는 이전 학습기들이 잘못 분류한 데이터 포인트들에 더 집중하여, 새로운 규칙을 추가할 때 이전의 결정들을 보완하려고 합니다. 그래디언트 부스팅: 그래디언트 부스팅은 이전 학습기의 잔차(실제 값과 예측 값의 차이)를 줄이는 방향으로 새로운 학습기를 추가합니다. 이 방법은 손실 함수의 그래디언트를 이용해 학습기를 순차적으로 추가하며, 각 단계에서는 이전 모든 단계의 합산 결과와의 차이(잔차)를 최소화하는 방향으로 학습합니다. 이러한 부스팅 기법들은 여러 약한 학습기를 결합하여 높은 정확도를 가진 강력한 모델을 만들어내는 효과적인 방법입니다.
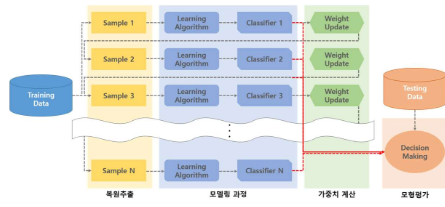
3.24 Adaboost (Adaptive boosting)
Adaboost (Adaptive Boosting)는 각 반복에서 훈련 예제들의 가중치를 재조정하여 이전 약한 학습기의 실수에서 배우는 강한 분류기를 구축하는 기법입니다. 이 방법은 각 단계에서 약한 학습기의 결과를 바탕으로 잘못 분류된 데이터에 더 많은 가중치를 부여하고, 이를 통해 모델이 이전의 실수를 극복하고 개선해 나가도록 합니다. 예를 들어, 앙상블이 세 번의 부스팅 라운드로만 구성되어 있다고 가정해 보겠습니다. 첫 번째 라운드에서는 초기 데이터 세트에 대해 약한 학습기가 훈련되고, 잘못 분류된 데이터 포인트들은 더 높은 가중치를 받습니다. 두 번째 라운드에서는 이러한 가중치가 적용된 새로운 데이터 세트에 대해 다시 학습이 이루어지며, 다시 한번 잘못 분류된 데이터에 더 높은 가중치를 부여합니다. 세 번째 라운드에서는 이 과정을 반복하여, 각 단계에서의 실수에서 배우며 전체적으로 더 강력한 분류기를 구축합니다. 이처럼 Adaboost는 반복적으로 가중치를 조정하고 학습함으로써, 각 단계에서의 약한 학습기들이 전체적으로 강한 분류기로 통합될 수 있게 합니다.
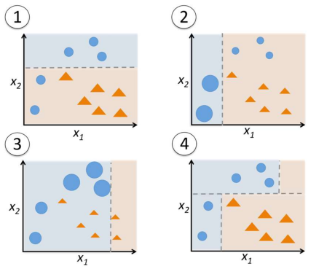
3.25 Gradient Boosting
Gradient Boosting은 부스팅의 인기 있는 변형입니다. AdaBoost와 Gradient Boosting은 약한 학습자(weak learners)를 강한 학습자(strong learners)로 향상시키는 주요 개념을 공유하지만, 가중치가 어떻게 업데이트되고 분류기가 어떻게 결합되는지에 대해 주로 차이가 있습니다. Gradient Boosting은 이전 학습자의 오차(실제 값과 예측 값 사이의 차이)를 줄이는 방향으로 새로운 학습자를 순차적으로 추가합니다. 이 방법은 손실 함수의 기울기를 사용하여 오차를 최소화하고자 합니다. 반면, AdaBoost는 잘못 분류된 데이터에 더 많은 가중치를 부여하여 학습자를 순차적으로 훈련시킵니다. XGBoost는 Gradient Boosting의 한 형태로, 기존 Gradient Boosting 대비 훨씬 빠른 속도로 주목받고 있습니다. XGBoost는 병렬 처리, 트리 가지치기, 가중치 정규화 등 다양한 기술적 최적화를 통해 높은 성능과 빠른 학습 속도를 제공합니다. 따라서 많은 데이터 과학자와 기계 학습 전문가들이 대규모 데이터 세트를 다룰 때 XGBoost를 선호합니다.
3.26 XGBoost
XGBoost는 Extreme Gradient Boosting의 약자로, 매우 효율적이고 유연하며 이식성이 뛰어난 분산 그래디언트 부스팅 라이브러리입니다. 이 기술은 구조화된(테이블 형태의) 데이터에 대한 Kaggle 대회를 포함하여 모든 주요 경쟁에서 우위를 차지했습니다. XGBoost는 다음과 같은 특징을 가지고 있습니다: 높은 효율성과 속도: XGBoost는 병렬 처리를 통해 학습과 예측을 가속화합니다. 또한, 고급 최적화 기술을 사용하여 자원 사용을 최소화하면서도 성능을 극대화합니다. 유연성: 사용자는 맞춤 손실 함수를 정의할 수 있으며, 이를 통해 다양한 종류의 예측 문제에 적용할 수 있습니다. 이식성: XGBoost는 Linux, Windows, macOS와 같은 다양한 운영 체제에서 사용할 수 있으며, Python, R, Java, Scala, Julia 등 여러 프로그래밍 언어를 지원합니다. XGBoost의 이러한 특징들은 데이터 과학자들이 구조화된 데이터 문제에 대해 높은 성능의 모델을 신속하게 개발할 수 있도록 돕습니다.
3.27 LightGBM
LightGBM은 트리 기반 학습 알고리즘을 사용하는 그래디언트 부스팅 프레임워크입니다. 분산되고 효율적인 설계를 갖추고 있으며, 다음과 같은 여러 장점을 제공합니다: 더 빠른 학습 속도와 높은 효율성: LightGBM은 기존 그래디언트 부스팅 대비 학습 시간을 크게 단축시키며, 높은 효율성을 자랑합니다. 낮은 메모리 사용량: 고도의 최적화를 통해, LightGBM은 적은 메모리로도 대규모 데이터를 처리할 수 있습니다. 더 나은 정확도: 고급 알고리즘과 최적화 기법을 사용하여, 더 높은 예측 정확도를 달성합니다. 병렬, 분산, GPU 학습 지원: 다양한 컴퓨팅 환경에서의 활용성을 높이기 위해, LightGBM은 병렬 처리, 분산 컴퓨팅, GPU 학습을 지원합니다. 대규모 데이터 처리 능력: LightGBM은 매우 큰 데이터 세트도 효과적으로 처리할 수 있도록 설계되었습니다. 이러한 장점으로 인해, LightGBM은 많은 데이터 과학자와 기계 학습 전문가들 사이에서 선호되는 그래디언트 부스팅 도구 중 하나로 자리 잡았습니다.



