[Classification 1] 3. Classification algorithms - Decision tree

Content

• Introduction to supervised learning approach
• Data split in supervised learning
• Classification algorithms
  • KNN & distance measures
  • Decision tree
  • Random Forest, Ensemble approach
  • SVM

3. Classification algorithms - Decision tree

3.1 Classification example

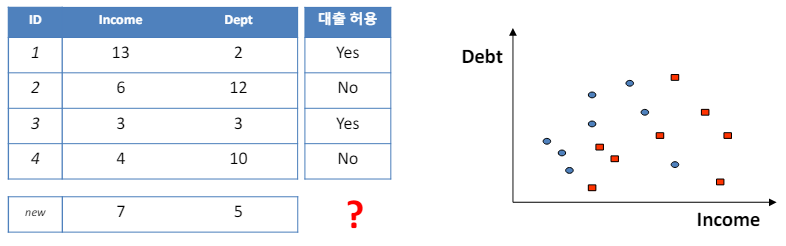
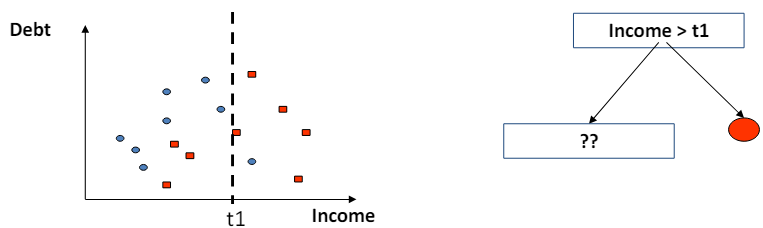
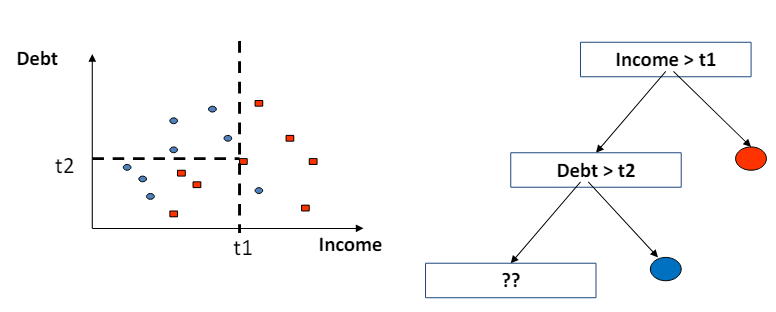
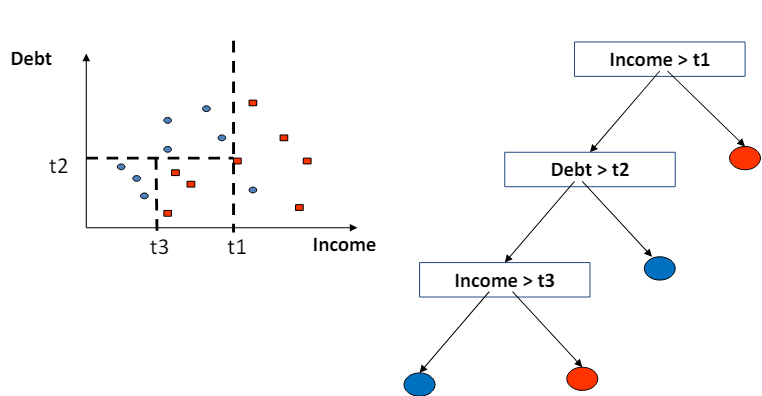
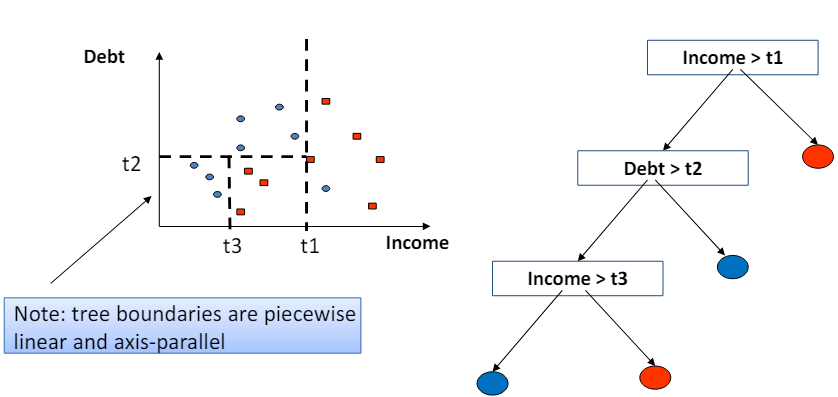
• 결정 트리의 경계는 조각별 선형(piecewise linear)이며 축에 평행(axis-parallel)하다는 것을 의미.
• 이는 결정 트리가 데이터를 분류하거나 회귀 분석을 할 때, 각 분할에서 사용하는 기준이 특정 특성(feature)의 값에 대해 수평이나 수직의 선으로 데이터를 나눈다는 것을 의미.
• 예를 들어, 어떤 결정 트리가 '무게'와 '색깔'이라는 두 가지 특성을 기반으로 데이터를 분류한다고 가정.
• 이때, 트리는 '무게 > 50g'과 같은 조건으로 데이터를 나누거나, '색깔 = 빨강'과 같은 조건으로 분류할 수 있다.
• 이러한 분할은 모두 축에 평행한 선으로 표현될 수 있으며, 이는 결정 트리에서 생성되는 경계가 조각별 선형이고 축에 평행함을 보여줌.
• 이러한 특성 덕분에 결정 트리는 해석하기 쉽다는 장점이 있지만, 데이터의 복잡한 패턴이나 비선형 관계를 포착하는 데는 한계가 있을 수 있다.

3.2 Understanding decision trees

• 결정 트리(Decision Trees)는 트리 구조 형태의 모델로, 데이터를 분류하거나 회귀 분석을 수행하는 데 사용.
• 노드(Node):
  • 결정 트리에서 노드는 데이터를 분리하는 결정이 이루어지는 지점.
  • 각 노드에서는 한 속성(attribute)에 대한 결정(예: 특정 속성이 특정 값을 초과하는가?)이 내려짐.
• Branch: 가지는 결정의 선택을 나타냄.
• 즉, 노드에서 내려진 결정에 따라 데이터가 어떤 방향으로 분리될지를 나타내는 경로입니다.
• 잎 노드(Leaf Node): 잎 노드는 결정의 조합 결과를 나타냅니다.
• 결정 트리의 마지막 단계에서, 데이터가 최종적으로 분류되거나 예측 값이 결정되는 지점입니다.
• 결정 트리는 '분할 정복(Divide and Conquer)' 접근 방식을 사용하여 구축됩니다.
• 이는 데이터를 더 작고 관리하기 쉬운 부분으로 나누어 각 부분에 대한 최적의 결정을 찾아내는 방식을 말합니다.
• 이 과정을 통해 결정 트리는 데이터의 복잡한 패턴을 간단하고 이해하기 쉬운 규칙으로 변환할 수 있습니다.
• 결정 트리는 그 구조가 단순하고 해석하기 쉽다는 장점이 있으나, 과적합(Overfitting)되기 쉽다는 단점도 있습니다.
• 따라서 결정 트리를 사용할 때는 적절한 가지치기(Pruning) 기법을 적용하여 모델의 일반화 능력을 높이는 것이 중요합니다.

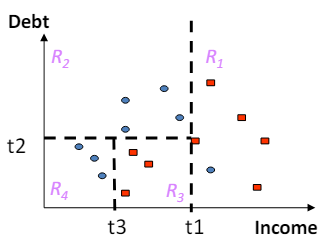
3.3 Partitioning up the predictor space

• 예측 변수 공간을 분할하는 것은 결정 트리나 다른 분류 및 회귀 모델을 사용할 때 중요한 단계입니다.
• 이 과정은 예측 변수 공간을 R1, R2, ..., Rk와 같은 구별되는 여러 영역으로 나누는 것을 포함합니다.
• 그 후, 특정 영역(예: Rj)에 속하는 모든 X에 대해 동일한 예측을 합니다.
• 이러한 예측 방식은 다음과 같이 두 가지 주요 접근 방식으로 나뉩니다:
• 다수결 투표 (Majority voting): 분류 문제에서 사용됩니다.
• 특정 영역 내의 훈련 데이터 중 가장 흔한 범주를 예측 결과로 선택합니다.
• 예를 들어, 어떤 영역 내에 '개'와 '고양이'라는 두 범주가 있고, '개'가 더 많다면 그 영역에 속하는 모든 데이터 포인트의 예측 결과는 '개'가 됩니다.
• 평균 응답 (Average of responses):
• 회귀 문제에서 사용됩니다.
• 특정 영역 내에 있는 모든 응답의 평균을 계산하여 예측값으로 사용합니다.
• 예를 들어, 어떤 영역 내의 모든 집 가격의 평균 값을 그 영역에 속하는 집의 가격 예측치로 사용합니다.
• 이러한 방식으로 예측 변수 공간을 분할하고 예측을 수행함으로써, 복잡한 데이터 구조를 간단하고 이해하기 쉬운 규칙으로 변환할 수 있습니다.
• 이는 데이터 내의 패턴을 파악하고, 새로운 데이터에 대한 예측을 제공하는 데 유용합니다.

3.4 Example: training Making predictions

데이터를 분할할 때, 주로 단일 클래스의 예시들로 구성된 파티션을 생성하는 특성 값을 찾는 것이 중요합니다. 이 과정은 특히 결정 트리와 같은 분류 알고리즘에서 중요한 역할을 합니다. 각 분할에서 가장 순수한(즉, 특정 클래스의 비율이 가장 높은) 파티션을 생성하기 위해 최적의 특성과 그 값을 선택합니다. 이를 통해 모델은 데이터 내의 복잡한 패턴을 단순화하여 학습할 수 있습니다. 예측을 하는 과정은 매우 간단합니다: 학습된 모델(결정 트리)의 최상단에서부터 시작하여, 주어진 데이터 포인트의 특성 값을 기반으로 결정 노드를 따라 내려갑니다. 각 분할 지점에서, 데이터 포인트가 속한 특성 값에 따라 왼쪽 또는 오른쪽 자식 노드로 이동합니다. 최종적으로 리프 노드(결정 트리의 가장 아래쪽에 있는 노드)에 도달하면, 그 노드에 할당된 클래스 레이블이나 값이 예측 결과가 됩니다. 계산 복잡도는 주로 모델을 학습하는 데에 있어서 고려됩니다. 모델을 한 번 학습시킨 후에는, 실제 예측을 수행하는 과정은 비교적 계산량이 적고 빠릅니다. 결정 트리의 경우, 예측에 필요한 계산 복잡도는 트리의 깊이에 비례합니다. 따라서, 트리가 깊어질수록 예측 시간이 늘어날 수 있지만, 일반적으로 다른 복잡한 머신러닝 모델에 비해 예측 속도가 빠른 편입니다.

3.5 Learning an optimal decision tree

최적의 결정 트리를 학습하는 과정에서 가장 중요한 질문 중 하나는 "어디에서 데이터를 분할할 것인가?"입니다. 1979년에 최적의 이진 결정 트리를 구축하는 것이 NP-완전 문제임이 밝혀졌습니다. 이는 결정 트리의 모든 가능한 구성을 탐색하여 최적의 해를 찾는 것이 계산상으로 매우 어렵다는 것을 의미합니다. 이러한 어려움에도 불구하고, 노드의 순도(impurity)를 기반으로 한 효율적인 근사 알고리즘들이 개발되었습니다. 이 알고리즘들은 데이터를 분할할 때 노드의 순도를 최대화하는 방향으로 작동합니다. 노드 순도를 측정하는 데 가장 일반적으로 사용되는 두 가지 방법은 엔트로피(Entropy)와 지니 지수(Gini index)입니다. 엔트로피: 데이터 세트의 불확실성 혹은 무질서도를 측정합니다. 엔트로피가 높으면 데이터 세트의 불확실성이 높은 것이며, 결정 트리는 이를 최소화하려고 합니다. 지니 지수: 불순도를 측정하는 또 다른 방법으로, 특정 노드에서 임의로 선택된 두 데이터 포인트가 다른 클래스에 속할 확률을 나타냅니다. 지니 지수가 낮을수록 노드의 순도가 높습니다. 이러한 기준을 사용하여 데이터를 분할하는 위치를 결정함으로써, 결정 트리는 분류 문제나 회귀 문제를 효과적으로 해결할 수 있는 모델을 구축할 수 있습니다. 그러나 완벽한 해를 찾는 것이 계산상 불가능하므로, 이러한 근사 방법을 사용하여 최적에 가까운 해를 찾습니다.

3.6 Node impurity

노드의 불순도(node impurity)란 해당 노드에서의 레이블들의 동질성을 측정하는 지표를 말합니다. 다시 말해, 불순도는 한 노드 내에 있는 데이터들이 얼마나 다른 클래스에 속해 있는지를 나타내는 척도입니다. 학습 알고리즘은 이 불순도를 최소화하는 방향, 즉 분할의 순도를 최대화하는 방향으로 파티션을 선택합니다. 불순도를 측정하는 방법으로는 주로 지니 지수(Gini index)와 엔트로피(Entropy)가 사용됩니다. 지니 지수(Gini index): 한 노드 내에서 무작위로 선택된 두 데이터가 다른 클래스에 속할 확률을 나타냅니다. 따라서 지니 지수가 낮을수록, 즉 0에 가까울수록 노드의 순도가 높다는 것을 의미하며, 노드가 해당 클래스의 데이터로만 구성되어 있음을 나타냅니다. 엔트로피(Entropy): 노드의 불확실성 또는 무질서를 측정합니다. 엔트로피가 높다는 것은 노드 내의 데이터가 여러 클래스에 걸쳐 있어 불확실성이 높다는 것을 의미합니다. 따라서 학습 알고리즘은 엔트로피를 최소화하는 방향으로 데이터를 분할하려고 합니다. 이러한 불순도 측정 방법을 통해 결정 트리는 가장 효율적인 방식으로 데이터를 분할하고, 각 노드에서의 예측을 보다 정확하게 할 수 있도록 합니다.

3.7 Gini index

Gini 지수는 CART(Classification And Regression Tree, 분류 및 회귀 트리) 알고리즘에 의해 사용되는 지표입니다. Gini 지수는 노드 내 모든 샘플이 단일 대상 클래스에 속할 때 최소값인 0에 도달합니다. 이는 해당 노드의 데이터가 완전히 동질적이라는 것을 의미하며, 따라서 불순도가 없다는 것을 나타냅니다. C개의 클래스를 가진 항목 집합에 대한 Gini 불순도는 다음과 같이 계산됩니다: [ Gini = 1 - \sum_{i=1}^{C} p_i^2 ] 여기서 (p_i)는 특정 클래스 i에 속하는 항목의 비율을 나타냅니다. 이 식은 각 클래스의 비율을 제곱하여 합산한 후 1에서 빼주는 방식으로 계산됩니다. 결과적으로, Gini 지수는 0(완전한 순수함)에서 1(최대 불순도) 사이의 값을 가지며, 노드의 데이터가 여러 클래스에 걸쳐 있을수록 더 높은 값을 가집니다. CART 알고리즘은 이 Gini 지수를 사용하여 데이터를 분할하는 최적의 방법을 찾습니다. 노드를 분할할 때마다 Gini 지수를 최소화하는 방향으로 분할을 결정함으로써, 분류 문제나 회귀 문제에 있어 더 정확한 예측을 가능하게 하는 트리를 구성하게 됩니다.

3.8 C5.0 algorithm

C5.0 알고리즘은 데이터 내의 순도(또는 순수성)를 측정하기 위해 엔트로피를 사용합니다. 엔트로피는 '무질서한 정도', '규칙적이지 않은 정도', '불확실성'을 나타내는 척도로, 데이터 내의 클래스 분포가 얼마나 균일한지를 나타냅니다. 엔트로피가 높을수록 데이터 내의 불확실성이 높고, 엔트로피가 낮을수록 데이터는 더 순수하다고 할 수 있습니다. 예를 들어, 두 클래스(0과 1)의 분포를 고려해보겠습니다: 예1: 클래스 0과 1의 분포가 각각 0.75와 0.25인 경우, 이 분포는 완전히 균일하지 않으므로 엔트로피는 0보다 크지만 최대값(1)보다는 작습니다. 예2: 클래스 0과 1의 분포가 각각 0.5와 0.5인 경우, 이 분포는 완전히 균일하므로 엔트로피가 최대값(1)에 도달합니다. 이는 데이터 내의 불확실성이 가장 높음을 의미합니다. 예3: 클래스의 분포가 1:0인 경우(모두 0이거나 모두 1), 이 분포는 완전히 순수하므로 엔트로피가 최소값(0)입니다. 이는 데이터 내에 불확실성이 전혀 없음을 의미합니다. C5.0 알고리즘은 이러한 엔트로피 개념을 사용하여 데이터를 분할할 때 가장 순도가 높은 방식을 선택합니다. 즉, 각 분할 후에 남는 하위 그룹의 엔트로피를 최소화하는 방향으로 데이터를 분할하여, 최종적으로 더 정확한 예측을 가능하게 하는 결정 트리를 구성합니다.

3.9 Impurity measures

• 불순도(impurity) 측정은 결정 트리와 같은 분류 알고리즘에서 데이터 집합의 균일도를 평가하는 방법입니다.
• 데이터 집합이 하나의 클래스로만 구성되어 있으면 균일하고 불순도가 0입니다.
• 반대로, 데이터 집합에 여러 클래스가 고르게 분포되어 있으면 불균일하고 불순도가 높습니다.
• 결정 트리는 불순도를 최소화하는 방향으로 데이터를 분할하여 정보의 균일성을 증가시키려고 합니다.
• 주로 사용되는 불순도 측정 방법에는 다음과 같은 것들이 있습니다:
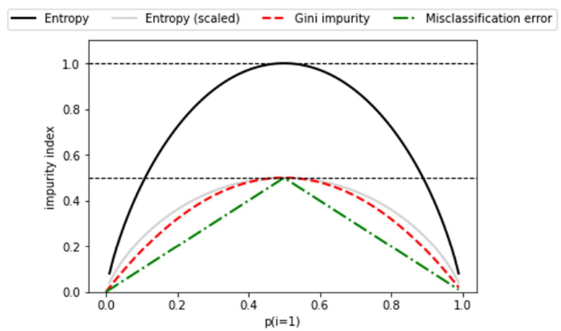
• 엔트로피(Entropy): 데이터 집합의 무질서도를 측정합니다.
• 엔트로피가 높으면 데이터 집합의 불확실성이 높고, 낮으면 불확실성이 낮습니다.
• 엔트로피는 다음 공식으로 계산됩니다: ( - \sum_{i=1}^{n} p_i \log_2(p_i) ), 여기서 (p_i)는 i번째 클래스의 비율입니다. 지니 불순도(Gini Impurity): 임의로 선택된 데이터가 잘못 분류될 확률을 측정합니다.
• 지니 불순도는 다음과 같이 계산됩니다: (1 - \sum_{i=1}^{n} p_i^2), 여기서 (p_i)는 i번째 클래스의 비율입니다.
• 분류 오류율(Classification Error): 잘못 분류될 최대 확률을 나타냅니다.
• 이는 다음 식으로 계산됩니다: (1 - \max(p_i)), 여기서 (p_i)는 i번째 클래스의 비율입니다.
• 이러한 불순도 측정 방법들은 결정 트리에서 최적의 분할을 찾는 데 사용됩니다.
• 데이터를 더 균일한 하위 집합으로 분할하는 특성을 찾기 위해, 각 분할 후의 불순도 감소량을 계산하여 가장 높은 정보 이득(또는 가장 낮은 불순도)을 제공하는 특성을 선택합니다.

3.10 Example: Decision tree

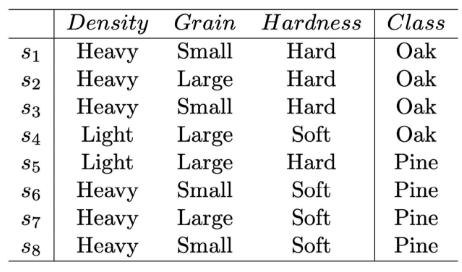
• 결정 트리에서 루트 노드로 선택할 특성을 결정하기 위해서는 정보 이득(Information Gain)이나 지니 불순도(Gini Impurity)와 같은 기준을 사용하여 각 특성이 얼마나 잘 데이터를 분류하는지 평가해야 합니다.
• 위의 예제에서 'density', 'grain', 'hardness' 세 가지 특성이 있으며, 이 중에서 가장 높은 정보 이득을 제공하거나 가장 낮은 지니 불순도를 가지는 특성이 루트 노드로 선택됩니다.
• 예제 데이터를 간략히 분석해보면, 'hardness' 특성이 'oak'와 'pine' 클래스를 구분하는 데 중요한 역할을 할 것으로 예상됩니다. 왜냐하면 'hard'인 샘플 중 대부분이 'oak'이고, 'soft'인 샘플은 모두 'pine'이기 때문.
• 하지만, 정확한 결정을 내리기 위해서는 각 특성에 대한 정보 이득을 계산하거나 지니 불순도를 측정해야 합니다.
• 실제 응용에서는 이러한 계산을 통해 가장 효율적으로 데이터를 분류할 수 있는 특성이 루트 노드로 선택되며, 이 과정은 결정 트리 알고리즘에 의해 자동으로 수행됩니다.
• 따라서, 가장 중요한 특성이 데이터의 구조를 이해하고 예측 모델을 구축하는 데 있어 핵심적인 역할

3.11 Node features

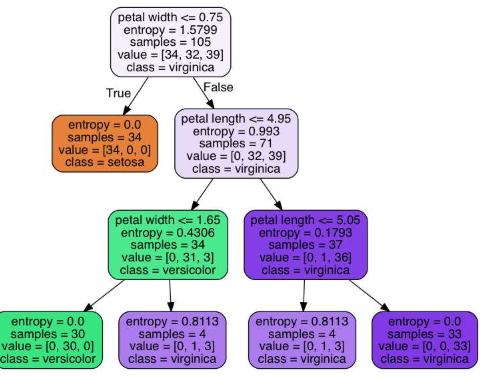
• 결정 트리에서 노드의 특성은 다음과 같은 정보를 포함합니다:
• 분할을 위한 특성과 임계값:
• 각 노드에서 데이터를 분할하기 위해 사용되는 특성(변수)과 그 특성을 기준으로 데이터를 분할하는 데 사용되는 임계값입니다. 불순도(엔트로피): 노드의 불순도는 해당 노드에 있는 데이터의 혼합 정도를 나타냅니다.
• 엔트로피는 불순도를 측정하는 한 방법으로, 값이 높을수록 데이터의 혼합 정도가 높다는 것을 의미합니다.
• 결정 트리는 불순도를 최소화하는 방향으로 데이터를 분할합니다.
• samples: 이 노드에 있는 총 샘플 수입니다.
• 즉, 이 노드를 통과하는 데이터 포인트의 수를 나타냅니다.
• value: 클래스별 샘플 수입니다. 이는 이 노드를 통과하는 각 클래스(또는 타겟 변수의 각 카테고리)에 속하는 샘플의 수를 나타냅니다.
• class: 이 노드에서의 다수결 클래스입니다.
• 즉, 이 노드에 있는 샘플 중 가장 많은 수를 차지하는 클래스를 말합니다.
• 결정 트리는 이러한 정보를 활용하여 데이터를 분할하고, 각 노드에서 최적의 분할을 결정하여 데이터를 효과적으로 분류하거나 예측합니다.

3.12 Information gain

• 정보 이득(Information gain)은 결정 트리에서 어떤 특성(Feature)으로 분할할지를 결정하는 데 사용되는 척도입니다.
• 정보 이득이 높다는 것은 해당 특성이 데이터를 더 균일한 그룹으로 나누는 데 더 효과적임을 의미합니다.
• 결정 트리는 데이터를 분류하거나 예측하는 모델을 만들 때, 각 단계에서 최적의 특성으로 데이터를 분할하여 정보의 불확실성을 최소화하는 방식으로 작동합니다.
• 정보 이득은 이러한 분할 전후의 엔트로피(데이터의 불확실성 또는 무질서도를 측정하는 척도) 차이를 기반으로 계산되며, 정보 이득이 높은 특성을 선택함으로써 더 순수한(동질적인) 하위 그룹을 생성할 수 있습니다.
• 따라서, 정보 이득이 높은 특성을 우선적으로 분할 기준으로 사용함으로써, 결정 트리의 예측 성능을 향상시키고, 모델의 복잡성을 줄일 수 있습니다.
• 이는 효율적인 학습 과정과 더 정확한 예측 결과로 이어집니다.

3.13 Building a decision tree

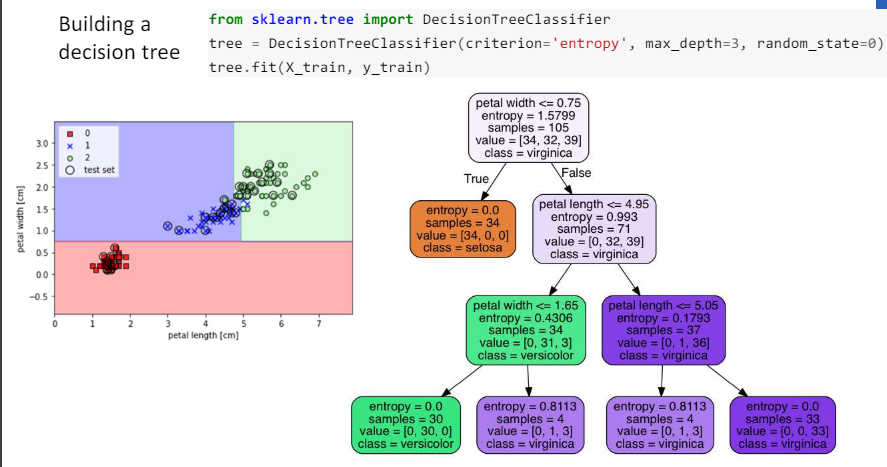
3.14 Tuning parameters (hyperparameters)

• max_depth 
• min_samples_split
• min_samples_leaf 
• max_leaf_nodes
• max_features

3.15 Example

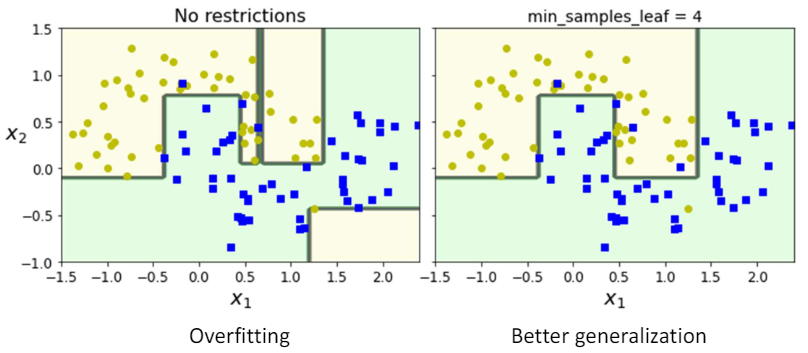
3.16 Pruning

• Pruning은 큰 트리(즉, 많은 단말 노드를 가진 트리)가 훈련 데이터에 과적합되는 경향이 있을 때, 이를 방지하기 위한 한 방법입니다.
• 과적합은 모델이 훈련 데이터에 너무 잘 맞춰져 있어서 새로운 데이터에 대한 일반화 능력이 떨어지는 현상을 말합니다.
• 이 문제를 해결하기 위해, 트리의 일부 단말 노드를 제거함으로써 모델의 복잡도를 줄이는 작업을 말합니다.
• 트리를 얼마나 되돌려야(prune) 할지 결정하기 위해서는, 교차 검증(cross validation)을 사용합니다.
• 교차 검증을 통해 다양한 크기의 트리에 대한 오류율을 비교함으로써, 가장 낮은 오류율을 보이는 트리 크기를 선택할 수 있습니다.
• 이 과정을 통해 모델의 일반화 능력을 향상시킬 수 있으며, 결과적으로 새로운 데이터에 대한 예측 정확도를 높일 수 있습니다.
• 결론적으로, pruning은 과적합을 방지하고 모델의 예측 성능을 최적화하는 중요한 과정입니다. 이를 통해 보다 간결하고 효율적인 결정 트리를 구성할 수 있습니다.

3.17 Example: Baseball Players’ Salaries

• 야구 선수들의 연봉을 분석할 때 결정 트리를 사용한다고 가정.
• 여기서 트리 크기가 3일 때 교차 검증(cross validation) 오류가 최소화된다는 것은, 결정 트리의 깊이나 복잡도를 3단계로 설정했을 때 모델이 데이터를 가장 잘 예측하고, 과적합(overfitting)이나 과소적합(underfitting)을 피하면서 가장 낮은 예측 오류를 보인다는 의미입니다.
• 이는 결정 트리가 너무 복잡하지 않으면서도 야구 선수들의 연봉을 결정하는 데 중요한 몇 가지 요소(예를 들어, 선수의 성적, 경험, 포지션 등)를 효과적으로 반영할 수 있다는 것을 시사합니다.
• 따라서, 이 경우 트리 크기를 3으로 설정하는 것이 가장 적절한 모델의 복잡도를 선택하는 것으로 볼 수 있습니다.
• 이러한 분석은 모델의 예측 성능을 최적화하고 실제 문제에 적용할 때 중요한 기준이 됩니

3.18 Why trees are useful in Practice

• 의사결정 트리가 실제로 유용한 이유는 다음과 같습니다: 고차원 데이터 처리 가능: 의사결정 트리는 여러 차원의 데이터를 효과적으로 처리할 수 있습니다. 이는 복잡한 데이터 세트에서도 유용하게 활용될 수 있음을 의미합니다. 대규모 데이터 세트에는 잘 확장되지 않음: 비록 의사결정 트리가 고차원 데이터를 처리할 수 있지만, 매우 큰 데이터 세트에 대해서는 트리를 구축하고 예측하는 데 필요한 계산 시간과 메모리가 증가하여 성능이 저하될 수 있습니다. 다양한 유형의 입력 변수 처리: 의사결정 트리는 숫자형 변수뿐만 아니라 범주형 변수도 처리할 수 있습니다. 대부분의 다른 머신러닝 방법들은 하나의 유형의 데이터를 요구하지만, 의사결정 트리는 이러한 제한 없이 다양한 유형의 데이터를 통합할 수 있습니다. 어느 정도 해석 가능: 의사결정 트리는 결과를 해석하기가 상대적으로 쉽습니다. 트리의 구조를 통해 어떤 변수가 예측에 중요한 역할을 하는지, 그리고 어떤 결정 경로가 결과에 이르는지를 직관적으로 이해할 수 있습니다.

3.19 Pros and Cons of Decision Trees

• 장점:
  • 설명하기 쉬움:
    • 결정 트리는 시각적으로 표현이 가능하며, 의사 결정 과정을 이해하기 쉬워 비전문가에게도 설명하기 용이.
  • 분류 및 회귀 문제에 모두 적용 가능:
    • 결정 트리는 분류 문제뿐만 아니라 회귀 문제에도 효과적으로 사용될 수 있어 다양한 데이터 세트와 문제에 적용할 수 있다.
• 단점:
  • 예측 정확도가 낮을 수 있음:
    • 결정 트리는 일부 복잡한 접근 방식에 비해 예측 정확도가 낮을 수 있다.
    • 이는 결정 트리가 단순한 구조로 인해 복잡한 패턴을 학습하는 데 한계가 있기 때문.
  • 높은 분산:
    • 결정 트리는 훈련 데이터에 대한 작은 변화에도 예측 결과가 크게 달라질 수 있어, 과적합(overfitting) 문제가 발생하기 쉽다.
    • 이는 모델의 일반화 능력이 떨어지게 만들 수 있다.
• 결정 트리는 그 구조와 해석의 용이성으로 인해 많은 분야에서 활용되고 있지만, 그 정확도와 일반화 능력에 있어서는 더 복잡한 모델에 비해 제한적일 수 있다는 점을 고려해야 함.
• 이러한 단점을 극복하기 위해 랜덤 포레스트나 그래디언트 부스팅과 같은 앙상블 기법이 사용되기도 함.

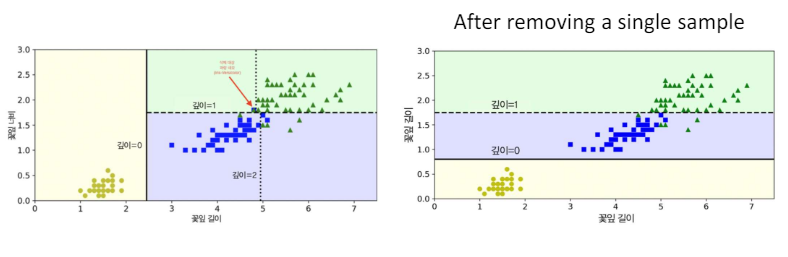
3.20 Example: high variance

• 예시
  • 높은 분산 훈련 결과가 훈련 세트의 변화에 매우 민감함.
    • 이는 모델이 훈련 데이터에 대해 과도하게 최적화되어 있으며, 이로 인해 새로운 데이터나 테스트 데이터에 대한 일반화 능력이 떨어지는 상황을 의미.
    • 훈련 세트의 작은 변화에도 훈련 결과가 크게 바뀌는 것은 모델이 훈련 데이터의 잡음이나 비현실적인 특성까지 학습해버렸다는 신호일 수 있다.
      • 이는 과적합(Overfitting)의 징후 중 하나로, 모델이 너무 복잡하거나 훈련 데이터에 특정되어 있을 때 발생할 수 있다.
  • 높은 분산 문제를 해결하기 위해서는 모델의 복잡도를 줄이거나, 더 많은 훈련 데이터를 확보하거나, 정규화 기법을 적용하는 등의 방법을 고려할 수 있다.
• 이러한 접근 방법은 모델이 훈련 데이터에 과도하게 의존하는 것을 방지하며, 새로운 데이터에 대해 더 잘 일반화할 수 있도록 도와줌.

3.21 Decision tree: summary

• Tree-based
• Interpretable
• Training & test phases 
• Pruning to get more ‘generalizable’ result 
• Decision boundary: