[Classification 1] 3. Classification algorithms - distance measures

Content

• Introduction to supervised learning approach
• Data split in supervised learning
• Classification algorithms
  • KNN & distance measures
  • Decision tree
  • Random Forest, Ensemble approach
  • SVM

DISTANCE MEASURE

3.14 Choice of Distance Measure

• 거리 측정 방식의 선택은 데이터와 애플리케이션에 따라 달라질 수 있으며, 각기 다른 특성과 용도를 가지고 있다.
• 일반적인 거리 측정 방식:
  • 유클리드 거리 (Euclidean distance):
    • 가장 일반적으로 사용되는 거리 측정 방식 중 하나로, 두 점 사이의 '직선 거리'를 계산.
    • 다차원 공간에서도 널리 사용.
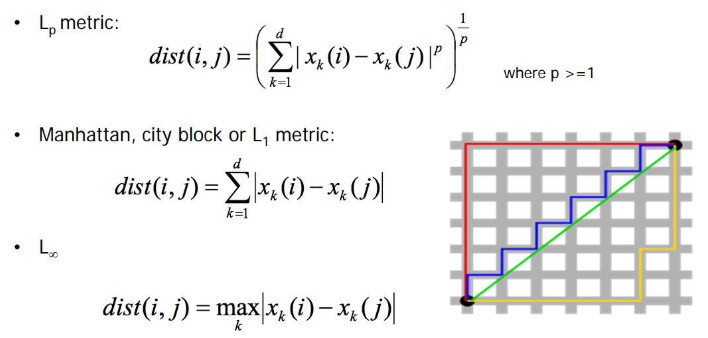
  • 맨해튼 거리 (Manhattan distance):
    • 격자구조에서 두 점 사이의 거리를 측정할 때 사용되며, '직각으로만 이동할 때의 거리'를 의미.
    • 이는 유클리드 거리보다 더 많은 경로를 고려.
  • Lp 노름 (Lp norm):
    • 거리 측정을 위한 일반화된 형태로, p값에 따라 다양한 거리 측정 방식을 표현할 수 있다.
    • 예를 들어, p=2일 때 유클리드 거리가 되고, p=1일 때 맨해튼 거리가 됨.
  • 마할라노비스 거리 (Mahalanobis distance):
    • 데이터의 분포를 고려하여 거리를 측정하는 방법으로, 변수들 간의 상관관계와 각 변수의 분산을 반영.
    • 이 방법은 변수들이 서로 독립적이지 않을 때 유용.
  • 1 - 상관관계 (1 - Correlation):
    • 두 변수 간의 상관관계를 기반으로 거리를 측정.
    • 상관관계가 높을수록 거리는 작아지고, 상관관계가 낮을수록 거리는 커짐.
  • 1 - 코사인 유사도 (1 - Cosine similarity):
    • 두 벡터 간의 각도를 기반으로 거리를 측정.
    • 이 방법은 텍스트 문서의 유사성 측정 등에 주로 사용.
• 각 거리 측정 방식은 데이터의 특성과 분석의 목적에 따라 선택.
• 예를 들어, 변수 간의 상관관계가 중요한 경우 마할라노비스 거리가 유용할 수 있고, 텍스트 데이터를 다룰 때는 코사인 유사도가 적합할 수 있다.
• 따라서, 사용할 거리 측정 방식을 결정하기 전에 데이터의 특성을 충분히 이해하는 것이 중요.

3.15 Euclidean Distance

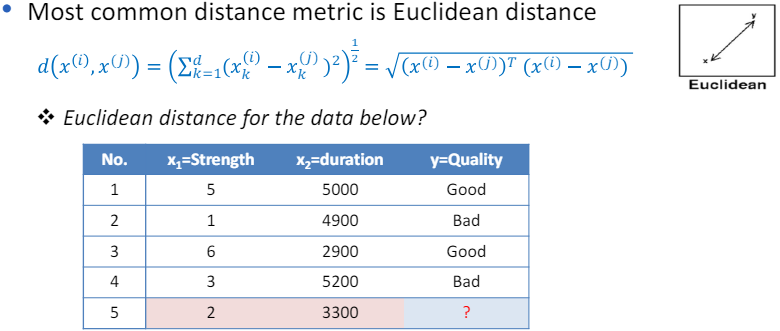
• 유클리드 거리는 가장 일반적으로 사용되는 거리 측정 방식 중 하나로, 두 점 사이의 "직선 거리"를 계산하는 방법.
• 데이터 포인트 간의 유클리드 거리를 계산하기 위해서는 다음 공식을 사용:
  • 여기서 (x_1, x_2)는 첫 번째 데이터 포인트의 두 변수 값이고, (y_1, y_2)는 두 번째 데이터 포인트의 두 변수 값.
• 제시된 데이터를 기준으로, 5번 데이터 포인트와 다른 데이터 포인트들 사이의 유클리드 거리를 계산.
• 5번 데이터 포인트의 값은 (x_1 = 2), (x_2 = 3300)입니다. 예를 들어, 1번 데이터 포인트와의 유클리드 거리를 계산해보겠습니다:
• 1번 데이터 포인트의 값은 (x_1 = 5), (x_2 = 5000)입니다.
• 이를 통해 5번 데이터 포인트가 다른 데이터 포인트들과 얼마나 떨어져 있는지를 수치적으로 파악할 수 있으며, 이 정보를 바탕으로 5번 데이터 포인트의 'quality'를 추론할 수 있습니다.
• 예를 들어, K-NN 알고리즘을 사용하여 가장 가까운 이웃의 'quality' 값을 기반으로 5번 데이터 포인트의 'quality'를 예측할 수 있습니다.
• 유클리디안 거리는 다양한 측정치들이 동일한 단위로 측정될 때 의미가 있습니다.
• 즉, 각 변수가 동일한 단위로 측정되는 경우에 유클리디안 거리를 사용하는 것이 타당합니다.
• 예를 들어, 모든 변수가 미터나 킬로그램과 같은 동일한 단위로 측정되는 경우, 유클리디안 거리를 사용하여 데이터 포인트 간의 거리를 측정할 수 있습니다.
• 그러나 측정치들이 다른 단위로 표현되는 경우, 예를 들어 길이가 미터와 인치로 표현되는 경우, 유클리디안 거리는 반드시 의미 있는 결과를 제공하지 않습니다.
• 이는 서로 다른 단위로 측정된 변수들이 동일한 비중으로 거리 계산에 반영되기 때문에, 실제로는 서로 다른 중요도를 가진 변수들이 동등하게 취급될 수 있기 때문입니다.
• 이런 문제를 해결하기 위해, 다른 단위로 측정된 데이터를 사용할 때는 정규화(normalization) 과정을 거치는 것이 중요합니다.
• 정규화는 데이터의 범위를 표준화하여 모든 변수가 동일한 척도로 비교될 수 있도록 조정하는 과정입니다.
• 예를 들어, 최소-최대 정규화(min-max normalization)나 z-점수 정규화(z-score normalization)와 같은 방법이 있습니다.
• 이렇게 정규화를 통해 변수들을 동일한 척도로 조정하면, 유클리디안 거리를 포함한 거리 측정 방법을 보다 의미 있게 사용할 수 있다.

3.16 Preprocessing: Normalization

• 데이터 전처리 과정에서 정규화(normalization)는 모델이 특성들을 공평하게 고려하도록 돕는 중요한 단계입니다.
• 여기서 주로 사용되는 정규화 방법에는 Z-점수 표준화, 최소-최대 정규화, 그리고 로버스트 스케일러가 있다.
• Z-점수 표준화 (StandardScaler):
• 이 방법은 각 특성의 평균을 0, 표준편차를 1로 조정.
• 이를 통해 모든 특성이 동일한 스케일을 갖게 되어, 특성 간 비교가 용이.
• 수학적으로는 각 데이터 포인트에서 평균을 빼고, 그 결과를 표준편차로 나누어 계산.
• 최소-최대 정규화 (MinMaxScaler): 이 방법은 데이터를 0과 1 사이의 범위로 조정합니다.
• 특정 특성의 최소값을 0, 최대값을 1로 설정하고, 나머지 값들을 이 범위 내에 선형적으로 변환합니다.
• 이 방식은 모든 특성이 동일한 범위를 갖게 하여, 모델이 특성을 공평하게 처리할 수 있도록 합니다.
• 로버스트 스케일러:
• 이 방법은 특성의 중앙값(median)을 0으로, IQR(Interquartile Range, 사분위수 범위)을 사용하여 데이터를 스케일링합니다.
• 로버스트 스케일러는 이상치(outliers)에 강한 내성을 가진다는 장점이 있습니다.
• 데이터에 이상치가 많은 경우, Z-점수 표준화나 최소-최대 정규화보다 로버스트 스케일러를 사용하는 것이 더 적합할 수 있습니다.
• 각 정규화 방법은 특정 상황에 따라 선택해 사용할 수 있으며, 모델의 성능과 특성들 간의 관계를 개선하는데 도움을 줍니다.

3.17 Extensions

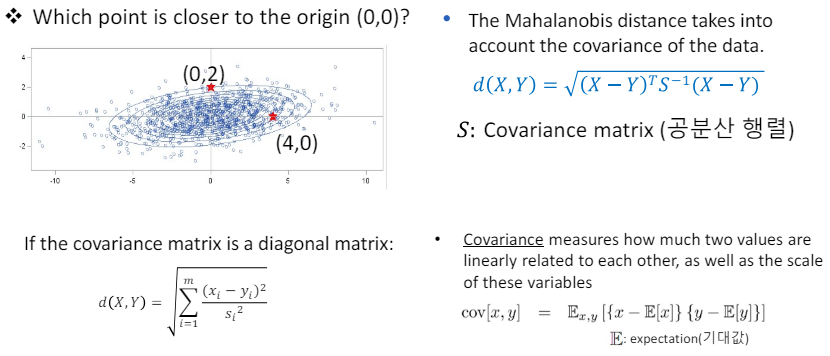
3.18 Mahalanobis distance

• 마할라노비스 거리는 데이터의 공분산을 고려하여 두 점 사이의 거리를 측정하는 방법입니다.
• 이 거리 측정법은 데이터의 분포를 고려하여, 특히 변수들 사이의 상관관계와 각 변수의 변동성을 반영합니다.
• 공분산 행렬(S)이 대각 행렬인 경우, 이는 각 변수가 서로 독립적이며, 변수들 사이에 선형 관계가 없음을 의미.
• 공분산은 두 변수가 얼마나 선형적으로 관련되어 있는지, 그리고 이 변수들의 스케일을 측정합니다.
• 공분산 행렬은 이러한 공분산들을 행렬 형태로 나타낸 것입니다.
• 마할라노비스 거리를 사용하여 원점(0,0)에 더 가까운 점을 찾으려면, 각 점의 마할라노비스 거리를 계산하고 비교해야 합니다.
• 마할라노비스 거리 계산 공식:
• 여기서 (D^2)는 마할라노비스 거리의 제곱을 나타내고, (x)는 점의 좌표, (\mu)는 평균 벡터(이 경우 원점이므로 0 벡터), (S^{-1})은 공분산 행렬의 역행렬입니다.
• 공분산 행렬이 대각 행렬이라면, 각 변수의 분산만이 거리 계산에 영향을 미치며, 변수들 사이의 상관관계는 고려되지 않습니다. 이는 각 변수가 독립적으로 거리에 기여함을 의미합니다.
• 따라서, 원점에 가까운 점을 찾으려면, 먼저 주어진 점들에 대해 마할라노비스 거리를 계산하고, 그 중 가장 작은 거리를 가진 점이 원점에 가장 가까운 점입니다.

3.19 Similarity measure: Correlation coefficient

3.20 Correlation coefficient

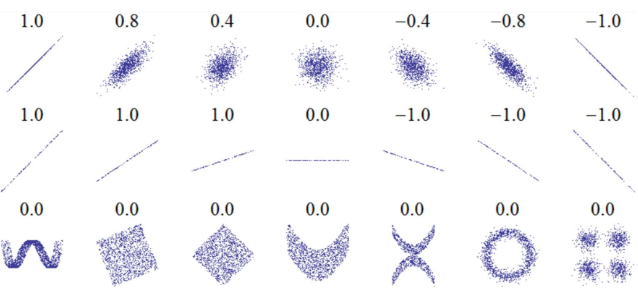
• 상관 계수(correlation coefficient)는 두 변수 간의 선형 관계의 강도와 방향을 나타내는 통계적 수치입니다.
• 이 값은 -1과 1 사이에 있으며, -1은 완벽한 음의 선형 관계, 1은 완벽한 양의 선형 관계를 나타내고, 0은 두 변수 간에 선형 관계가 없음을 의미합니다.
• 상관 계수는 두 변수의 관계가 선형적인지를 반영하지만, 그 관계의 기울기(slope)나 비선형적인 관계의 여러 측면은 반영하지 않습니다.
• 예를 들어, 상관 계수가 높다고 해서 한 변수의 변화가 다른 변수의 변화를 크게 일으키는 것은 아니며, 단지 두 변수 간에 일정한 방향성을 가지는 선형적인 관계가 있다는 것을 의미합니다.
• 선형 관계의 노이즈와 방향성(상단): 상관 계수는 데이터의 분포가 선형적인 경향을 가지고 있는지, 그리고 그 관계가 양의 방향인지 음의 방향인지를 반영합니다.
• 하지만, 데이터 포인트들이 선형 추세선을 얼마나 밀접하게 따르는지(노이즈의 정도)와는 무관하게 계산됩니다. 기울기(중단): 상관 계수는 두 변수 간의 관계의 기울기를 반영하지 않습니다.
• 즉, 두 변수가 완벽한 선형 관계를 가지더라도, 그 기울기가 완만하든 급격하든 상관 계수에는 영향을 미치지 않습니다.
• 비선형적 관계(하단): 만약 두 변수 간의 관계가 비선형적이라면, 상관 계수는 이를 적절히 반영하지 못할 수 있습니다.
• 예를 들어, 변수 간의 관계가 U자 형태나 파동 형태로 나타나는 경우, 상관 계수는 이러한 비선형적 관계의 복잡성을 잘 포착하지 못합니다.
• 따라서, 상관 계수를 해석할 때는 이러한 제한 사항을 고려해야 하며, 가능한 한 데이터를 시각화하거나 추가적인 분석을 통해 두 변수 간의 관계를 보다 정확히 이해하는 것이 중요합니다.

3.21 Cosine similarity

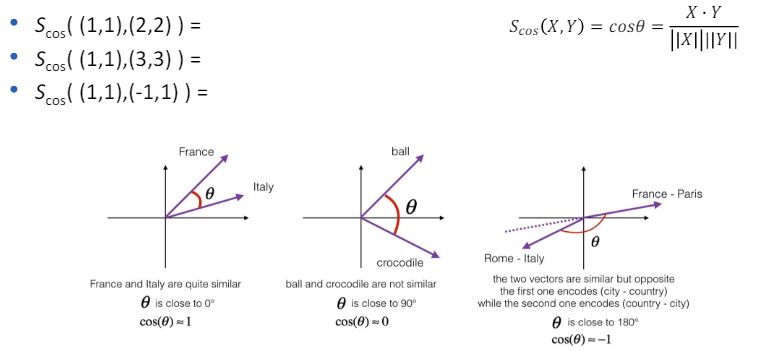
• 코사인 유사도는 두 벡터 간의 방향성만을 고려하여 그 유사도를 측정하는 방법입니다.
• 이는 두 벡터의 크기(마그니튜드)가 아닌 방향성이 얼마나 유사한지를 나타내기 때문에, 특히 텍스트 문서의 유사성 비교나 추천 시스템에서 널리 사용됩니다.
• 코사인 유사도의 값은 -1과 1 사이에 있으며, 값이 1에 가까울수록 두 벡터의 방향성이 유사함을 의미하고, -1에 가까울수록 방향성이 반대임을 나타냅니다.
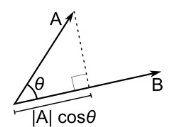
• 0은 두 벡터가 서로 직교한다는 것을 의미합니다. 코사인 유사도를 계산하는 공식은 다음과 같습니다: [ \text{코사인 유사도} = \frac{A \cdot B}{|A||B|} ]
• 여기서 (A \cdot B)는 두 벡터의 내적(점곱)을 의미하고, (|A|)와 (|B|)는 각각 벡터 (A)와 (B)의 크기(노름)를 나타냅니다.
• 내적은 두 벡터 각 요소의 상응하는 곱의 합으로 계산되며, 벡터의 크기는 벡터의 각 요소 값의 제곱합의 제곱근으로 계산됩니다.
• 코사인 유사도를 사용함으로써, 벡터의 크기에 영향을 받지 않고 두 벡터 간의 방향성만을 고려하여 유사성을 측정할 수 있습니다.
• 이는 예를 들어 문서 간의 유사성을 비교할 때, 문서의 길이와 무관하게 내용의 유사성을 평가할 수 있게 해줍니다.

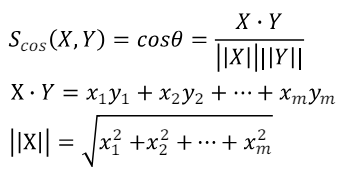
3.22 Cosine similarity: Example