반응형
Content
DataData quality- Exploratory data analysis
- Numerical summary
- Graphical summary
3.1 Exploratory Data Analysis (EDA)
- 탐색적 데이터 분석(Exploratory Data Analysis, EDA)은 데이터에 대한 일반적인 이해를 얻기 위해 수행하는 과정.
- 이 과정은 데이터 분석의 초기 단계에서 특히 유용
- detect outliers (e.g., assess data quality)
- 데이터의 질을 평가하고 이상치를 감지.
- 이를 통해 데이터가 분석에 적합한지 평가.
- test assumptions
- 가정을 검증.
- 예를 들어, 데이터가 정규 분포를 따르는지, 아니면 치우친 분포를 가지는지 확인할 수 있다.
- identify useful raw data & transforms
- 유용한 원시 데이터 및 데이터 변환을 식별.
- 예를 들어, 로그 변환(log(x))과 같은 변환을 통해 데이터를 더 잘 이해하고 분석할 수 있다.
- detect outliers (e.g., assess data quality)
- EDA는 모든 변수를 살펴보는 것을 포함.
- 이 과정에서 데이터의 각 변수를 분석함으로써, 데이터에 대한 깊은 이해를 얻을 수 있으며, 때로는 예상치 못한 통찰력을 얻을 수도 있습니다.
- 그림, 차트, 요약 통계 등 다양한 방법을 사용하여 데이터를 시각화하고 분석.
- 이러한 접근법은 데이터의 패턴, 이상치, 관계 등을 직관적으로 파악하는 데 도움.
- 수치적 요약 ( Numerical summaries of data - Descriptive statistics):
- 이 방법은 데이터의 기본적인 특성을 요약하는 데 사용.
- 평균, 중앙값, 분산, 표준편차와 같은 기술 통계를 통해 데이터의 중심 경향, 분포의 넓이 및 형태 등을 파악할 수 있다.
- 또한, 최소값, 최대값, 사분위수 등의 요약 통계를 사용하여 데이터의 범위와 이상값의 존재 여부를 확인할 수 있다.
- 그래픽 요약 ( Graphical summaries of data - Visualization):
- 데이터의 시각화는 데이터를 직관적으로 이해하는 데 도움.
- 히스토그램, 상자 그림(box plots), 산점도(scatter plots) 및 기타 그래픽 요소를 사용하여 데이터의 분포, 관계, 패턴 및 이상값을 시각적으로 탐색할 수 있다.
- 이러한 그래픽 요약은 복잡한 데이터 세트 내에서 숨겨진 경향성을 발견하고, 변수 간의 관계를 파악하며, 데이터 전처리 과정에서 중요한 결정을 내리는 데 중요한 역할.
3.2 Numerical Summaries of Data
- 데이터의 수치적 요약은 시각적 요소 없이 데이터의 기본적인 특성을 요약하는 방법.
- 주요 요약 통계:
- 평균(mean)과 중앙값(median): 데이터의 중심 경향.
- 최빈값(mode): 데이터에서 가장 자주 나타나는 값.
- 분산(variance)과 표준편차(standard deviation): 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 분포의 측도.
- 사분위수(quartiles): 데이터를 네 등분한 값으로, 분포의 범위와 이상치를 파악하는 데 유용.
- 범주형 변수의 고유값 수: 범주형 변수에서 각 범주의 고유한 값의 개수를 나타냄.
- 모든 요약 통계를 반드시 보고할 필요는 없다.
- 중요한 것은 이러한 수치들이 데이터에 대한 정확하고 의미 있는 정보를 제공하는지 여부.
- 데이터를 분석할 때 이러한 요약 통계가 데이터의 특성을 적절히 반영하고 있는지, 그리고 분석 목적에 부합하는지를 검토해야 함.
3.3 The average is not a good representation of the true center of the data
- 평균이 데이터의 진정한 중심을 잘 나타내지 못하는 경우가 있다.
- 예를 들어, 시험 점수가 9, 8, 7, 6, 5, 4, 3, 2, 1, 100인 10명의 학생이 있다고 가정.
- 이 데이터의 평균 점수는 14.5.
- 그러나 이 평균값은 실제 데이터 분포를 잘 반영하지 못함.
- 대부분의 학생들의 점수는 10점 미만이지만, 하나의 매우 높은 점수(100점) 때문에 평균값이 크게 올라감.
- 이러한 예시는 데이터 분포가 가우시안(정규분포)에서 멀리 떨어져 있을 때 특히 더 문제.
- 데이터에 극단적인 값이나 이상치가 포함되어 있을 경우, 평균은 데이터의 중심을 왜곡시키는 경향이 있다.
- 이런 상황에서는 중앙값이 더 나은 '중심' 지표가 될 수 있다.
- 중앙값은 데이터를 오름차순으로 정렬했을 때 가운데 위치한 값으로, 이상치의 영향을 덜 받기 때문에 데이터의 중심을 더 잘 나타내줌.
- 따라서 데이터의 분포를 파악하고, 평균이 데이터의 중심을 적절히 나타내는지 여부를 항상 고려하는 것이 중요.
- 데이터에 이상치가 존재하거나 분포가 비대칭적일 경우, 평균 대신 다른 요약 통계량을 사용하는 것이 더 적절할 수 있다.

3.4 Median
- 중앙값은 데이터를 오름차순으로 정렬했을 때 정확히 가운데에 위치하는 값을 말함.
- 데이터가 비대칭적으로 분포되어 있거나 이상치가 포함된 경우에 특히 유용.
- 중앙값은 평균보다 더 강건한 통계치.
- 즉, 이상치의 영향을 덜 받기 때문에 데이터의 중심을 더 잘 나타낼 수 있다.
- 하지만 중앙값은 이론적으로 다루기가 어렵다.
- 평균과 달리 중앙값을 계산하기 위한 간단한 수학적 공식이 없기 때문.
- 데이터의 개수가 홀수인 경우에는 가운데 값이 중앙값이 되지만, 짝수인 경우에는 가운데에 위치한 두 값의 평균을 중앙값으로 사용.
- 따라서 데이터 분석에서 중앙값은 분포가 극단적으로 치우쳐 있거나, 이상치가 존재할 때 데이터의 중심을 더 정확하게 파악하는데 도움.
- 그러나 이론적인 분석이나 수학적 처리가 필요할 때는 중앙값보다는 다른 통계치를 사용하는 것이 더 적합할 수 있다.
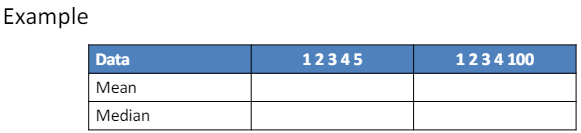
3.5 Percentiles (a.k.a Quantiles)
- 백분위수(또는 분위수)는 관측값의 n%가 해당 값 이하로 떨어지는 값을 의미.
- 이는 데이터 집합을 백분율로 나누어 위치를 파악할 수 있는 방법.
- Q1(25번째 백분위수 또는 첫 번째/하위 분위수):
- 데이터의 25%가 이 값 이하로 떨어짐.
- Q2(중앙값 또는 50번째 백분위수):
- 데이터의 50%가 이 값 이하로 떨어지며, 중앙값이라고도 함.
- Q3(75번째 백분위수 또는 세 번째/상위 분위수):
- 데이터의 75%가 이 값 이하로 떨어짐.
- 사분위 범위(IQR)는 하위 분위수(Q1)와 상위 분위수(Q3)의 차이로 계산되며, 데이터의 중간 50%의 범위를 나타냄.
- 즉, 25%부터 75%까지의 범위, 즉 Q3에서 Q1을 뺀 값. IQR은 데이터의 분포를 이해하고 이상치를 감지하는 데 유용
- 데이터의 중앙 부분이 얼마나 퍼져 있는지를 보여줌.
- Q1(25번째 백분위수 또는 첫 번째/하위 분위수):
3.6 Graphical summary of data
- 데이터의 그래픽 요약은 데이터를 시각적으로 표현하여 이해하는 방법.
- 주로 수치형 변수의 분포와 관계를 파악하기 위해 사용.
- 박스플롯(Boxplot):
- 다섯 숫자 요약(최솟값, 제1사분위수(Q1), 중앙값(Q2), 제3사분위수(Q3), 최댓값)을 시각화하는 일반적인 방법.
- 박스플롯은 데이터의 분포, 중앙값, 이상치를 한눈에 파악할 수 있게 해줌.
- 박스의 중앙에 있는 선은 중앙값을 표시하고, 박스의 길이는 사분위수 범위(IQR)를 나타내며, 박스 바깥의 점들은 이상치를 나타냄.
- 히스토그램(Histogram):
- 수치형 변수의 분포를 그래프로 나타내는 또 다른 방법.
- 데이터를 여러 구간으로 나누고, 각 구간에 속하는 데이터의 개수를 막대로 표시하여 데이터의 분포와 형태를 파악할 수 있다.
- 히스토그램은 데이터가 얼마나 집중되어 있는지, 어떤 형태의 분포를 가지고 있는지 시각적으로 이해하기 쉽게 해줌.
- 박스플롯(Boxplot):
- 데이터의 질을 확인하고 가정을 검증하기 위해 그래픽 요약을 사용.
- 데이터 분석을 시작할 때는 우선 단변수(Univariate) 요약부터 시작하여 데이터의 개별적인 특성을 이해하고, 그 다음에는 변수 간의 관계를 고려하기 시작.
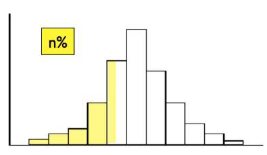
3.7 Boxplot
- Boxplot(상자 그림)은 데이터의 분포와 이상치를 시각적으로 표현하는 데 유용한 그래픽 요약 방법.
- 이는 특히 범주형 변수와 수치형 변수가 결합된 데이터를 분석할 때 유용.
- x축:
- 범주형 변수가 위치.
- 이는 데이터를 그룹화하는 기준.
- y축:
- 실수 값이나 정수 값을 가진 수치형 변수가 위치.
- 이 변수의 분포를 통해 각 그룹의 통계적 특성을 비교 분석할 수 있다.
- Boxplot에서 각 그룹에 대해 다음과 같은 정보를 제공:
- 중앙값(Median):
- 데이터의 중앙에 위치한 값으로, 상자 그림에서 상자의 가운데 선으로 표시.
- 사분위 범위(IQR; Interquartile Range):
- 25%에서 75% 범위에 해당하는 데이터의 분포를 나타내며, 상자의 길이로 표현.
- 이는 데이터의 중앙 50%를 나타내며, 데이터의 분산 정도를 파악할 수 있다.
- 수염(Whiskers):
- 상자 바깥의 선으로, 일반적으로 IQR의 1.5배 범위 내에서 가장 극단적인 값(이상치로 간주되지 않는)까지 표시.
- 수염의 끝은 해당 범위 내에서의 최소값과 최대값을 나타냄.
- 이상치(Outliers):
- 수염의 범위를 벗어난 데이터 포인트로, 일반적으로 수염의 끝에서 1.5*IQR 이상 떨어진 값으로 표시.
- 이상치는 데이터에서 특별히 주의해야 할 부분을 나타내며, 점으로 표시.
- 중앙값(Median):
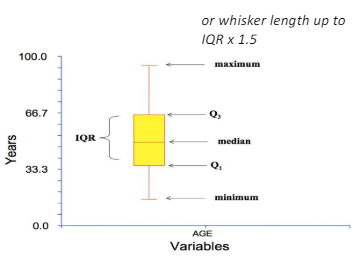
3.8 Box (and Whisker) Plots - Pima Indian data
- Boxplot은 데이터의 분포를 한눈에 파악하고, 그룹 간 비교를 용이하게 하며, 이상치를 식별하는 데 유용.
3.9 Histograms
- 히스토그램은 수치 데이터의 분포를 시각화하는 데 사용되는 그래픽 도구.
- 데이터의 분포를 이해하고, 데이터가 어떤 형태를 가지고 있는지 파악하는 데 유용.
- 히스토그램을 그리는 과정:
- 데이터 범위를 동일한 크기의 구간(빈)으로 나눔.
- 이때 구간의 수나 크기는 분석자가 결정할 수 있으며, 데이터의 특성과 분석 목적에 따라 조정될 수 있다.
- 각 구간에 속하는 데이터 포인트의 수를 세어봄.
- 이 과정을 통해 각 구간에 데이터가 얼마나 많이 분포하는지 알 수 있다.
- x축에는 변수의 값들을, y축에는 빈도(각 구간의 데이터 포인트 수) 또는 비율을 표시.
- 빈도는 각 구간에 속하는 데이터 포인트의 수를, 비율은 전체 데이터 중 해당 구간에 속하는 데이터의 비율을 의미.
- 데이터 범위를 동일한 크기의 구간(빈)으로 나눔.
- 히스토그램을 통해 데이터의 분포 모양을 분석할 수 있다.
- 예를 들어, 데이터가 정규 분포를 따르는지, 어떤 구간에 데이터가 집중되어 있는지, 이상치가 있는지 등을 시각적으로 파악할 수 있다.
- 또한, 데이터의 중심 경향성, 분산의 정도, 왜도 및 첨도 등을 대략적으로 추정할 수 있다.

3.10 Histogram detecting outliers

3.11 Shape of histograms
- 히스토그램의 형태를 확인하는 것은 데이터 분포의 전반적인 모양과 특성을 이해하는 데 중요.
- 데이터 분포의 형태를 통해 다음과 같은 특성을 파악할 수 있다:
- 정규성 (Normality):
- 데이터가 정규 분포를 따르는지 여부를 확인할 수 있다.
- 정규 분포는 종 모양의 대칭적인 형태를 가지며, 대부분의 데이터가 평균 주변에 집중되어 있다.
- 왜도 (Skewness):
- 데이터의 비대칭도를 나타냄.
- 오른쪽으로 긴 꼬리를 가지면 우측 왜도(positive skew), 왼쪽으로 긴 꼬리를 가지면 좌측 왜도(negative skew)로 불림.
- 왜도는 데이터의 분포가 중심값을 중심으로 어느 한쪽으로 치우쳐 있는지를 보여줌.
- 첨도 (Kurtosis):
- 데이터 분포의 뾰족함을 나타냄.
- 높은 첨도는 데이터가 평균 주변에 더 많이 집중되어 있음을 의미하며, 낮은 첨도는 데이터가 더 평평하게 분포되어 있음을 의미.
- 균일성 (Uniformity):
- 모든 값이 비슷한 빈도로 발생하는지를 나타냄.
- 균일 분포에서는 히스토그램의 모든 막대가 거의 같은 높이를 가짐.
- 이중 모드 (Bimodality) 또는 다중 모드 (Multimodality):
- 데이터에 두 개 이상의 뚜렷한 최빈값이 있는지 확인.
- 이는 데이터가 여러 그룹으로 구성될 수 있음을 시사할 수 있다.
- 정규성 (Normality):

3.12 Issues with Histograms
- 그러나 히스토그램을 사용할 때 몇 가지 주의해야 할 점:
- 대규모 데이터 세트에 효과적:
- 대규모 데이터 세트의 경우, 히스토그램은 분포의 일반적인 속성을 효과적으로 보여줄 수 있다.
- 데이터가 많을수록 히스토그램은 더 정확한 분포 형태를 나타낼 수 있다.
- 소규모 데이터 세트에는 오해의 소지가 있음:
- 소규모 데이터 세트의 경우, 히스토그램이 혼란을 줄 수 있다.
- 데이터 포인트가 적을 때는 무작위 변동성이 결과를 크게 왜곡할 수 있으며, 이는 분포의 실제 특성을 잘못 해석하게 만들 수 있다.
- 단일 변수에만 효과적:
- 히스토그램은 한 번에 하나의 변수만 시각화할 수 있으므로, 여러 변수 간의 관계나 상호작용을 탐색하고자 할 때는 다른 시각화 도구를 사용해야 함.
- 히스토그램 스무딩:
- 데이터의 분포를 더 부드럽게 표현하기 위해 다양한 스무딩 기법을 사용할 수 있다.
- 스무딩은 임의의 변동성을 줄이고 데이터의 전반적인 경향성을 더 명확하게 보여주는 데 도움이 될 수 있다.
- 스무딩 기법으로는 커널 밀도 추정(KDE)이나 다항식 스무딩 등이 있다.
- 대규모 데이터 세트에 효과적:
- 히스토그램을 사용할 때 이러한 제한 사항을 인식하고 적절히 대응하는 것이 중요.
- 데이터의 특성과 분석 목적에 따라 히스토그램의 매개변수(예: 빈의 크기와 수)를 조정하거나, 필요한 경우 다른 시각화 기법을 병행하여 사용하는 것이 좋다.
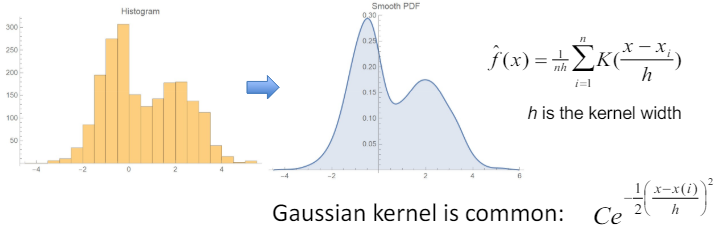
3.13 Smoothed Histograms - Density Estimates
- 히스토그램을 부드럽게 만드는 한 방법은 커널 밀도 추정(Kernel Density Estimate, KDE)을 사용하는 것.
- 커널 밀도 추정은 각 데이터 포인트의 영향을 해당 점 주변의 로컬 이웃에 걸쳐 부드럽게 퍼뜨리는 방식으로 작동함.
- 이는 데이터 포인트가 단순히 단일 구간(bin)에만 포함되는 대신, 주변 구간에도 영향을 미치도록 하여 전체 분포를 더 부드럽고 연속적으로 표현할 수 있게 함.
- 커널 함수는 데이터 포인트 주변의 가중치를 결정하는 데 사용되며, 가우시안(정규분포) 커널이 일반적으로 사용됨.
- 커널의 폭(밴드폭)은 추정된 밀도의 부드러움을 결정하는 중요한 요소
- 밴드폭이 너무 좁으면 추정이 데이터에 너무 민감해짐
- 너무 넓으면 과도하게 부드러워져 실제 데이터 구조를 잃어버릴 수 있다.
- 결과적으로, 커널 밀도 추정을 사용한 부드러운 히스토그램은 데이터의 전체적인 분포와 패턴을 더 명확하게 파악할 수 있게 해주며, 특히 데이터의 분포가 복잡하거나 다중 모드일 때 유용.
반응형
'Computer Science > 기계학습' 카테고리의 다른 글
| [Classification 1] 2. Data split in supervised learning (0) | 2024.04.21 |
|---|---|
| [Classification 1] 1. Introduction to supervised learning approach (0) | 2024.04.21 |
| [Exploratory Data Analysis] 3. Exploratory data analysis (2) (0) | 2024.04.21 |
| [Exploratory Data Analysis] 2. Data quality (0) | 2024.04.20 |
| [Exploratory Data Analysis] 1. DATA (0) | 2024.04.20 |



