Digital Systems and Logic (1) 논리 게이트, 조합 및 순차 논리, ALU, 그리고 불 대수

1. Hardware Design Hierarchy

2. 스위치

• 스위치는 물리적 구현의 기본 요소.
• 관례적으로 입력이 "1"일 경우, 스위치가 활성화(asserted)된 것으로 간주.
  • 만약 A가 "0"(비활성화, unasserted)인 경우, 스위치를 열고(Open) 전구(Z)를 끈다(OFF).
  • 만약 A가 "1"(활성화, asserted)인 경우, 스위치를 닫고(Close) 전구(Z)를 켠다(ON).
    • 즉, 입력 신호 A의 값에 따라 스위치의 상태가 결정되고, 이에 따라 전구 Z의 켜짐/꺼짐 상태가 제어됨.

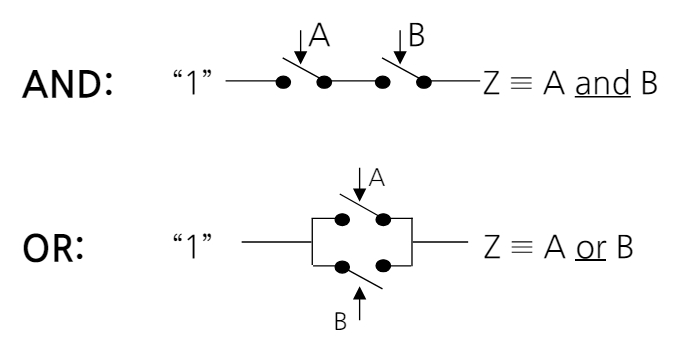
• 스위치들을 더 복잡한 구조(부울 함수)로 구성할 수 있다.
• 화살표는 어설션(확신) 시의 동작을 나타냄(1=닫힘).
  • 즉, 스위치들을 조합하여 더 복잡한 논리 기능을 수행할 수 있으며, 이러한 구조에서는 입력 신호의 어설션이 스위치의 동작(예를 들어, 닫힘)을 결정하게 됨.
    • 이를 통해 복잡한 부울(Boolean) 함수를 물리적으로 구현할 수 있다.
• 화살표는 이러한 동작이 어떻게 이루어지는지를 나타내주며, 예를 들어, 입력이 1일 때 스위치가 닫히는 방식으로 표현됨.

3. Block Diagrams

• 실제로, 칩은 단지 트랜지스터와 전선으로 구성.
• 트랜지스터의 소규모 그룹은 유용한 구성 요소를 형성하며, 이를 결합하여 더 높은 수준의 블록을 구축할 수 있다.
• NAND만으로 AND, OR, NOT을 구축할 수 있다.
  • 즉, 복잡한 전자 회로나 칩의 설계에서는 트랜지스터 같은 기본적인 구성 요소들을 조합하여 논리적 기능을 수행하는 더 복잡한 블록을 만든다.
    • 예를 들어, NAND 게이트는 매우 기본적인 구성 요소지만, 이를 적절히 연결함으로써 AND, OR, NOT 같은 다른 논리 연산을 수행할 수 있는 구조를 만들 수 있다.
    • 이러한 방식으로, 단순한 구성 요소들을 활용하여 복잡한 로직 회로를 설계할 수 있다.

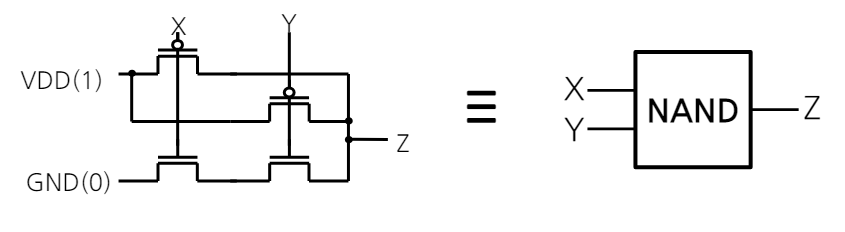
4. Type of Circuits

• 디지털 시스템은 두 가지 기본 유형의 회로로 구성.
• 조합 논리(Combinational Logic) 출력이 현재 입력에만 의존.
  • 예를 들어, A와 B를 더하는 회로(ALU - Arithmetic Logic Units)가 이에 해당.
• 순차 논리(Sequential Logic) 출력이 현재 입력과 현재 상태(저장된 값)에 의존.
  • 메모리 요소를 포함.
  • 예를 들어, 메모리와 레지스터가 이에 해당.
    • 간단히 말해, 디지털 시스템의 회로는 입력만을 기반으로 출력을 결정하는 조합 논리와, 이전의 상태 또는 저장된 정보를 함께 고려하여 출력을 결정하는 순차 논리로 나뉜다.

5. ALU (Arithmetic Logic Unit)

• ALU는 정수 이진수에 대해 산술 및 비트 단위 연산을 수행하는 조합 디지털 전자 회로.
• ALU는 컴퓨터의 CPU, FPU, GPU를 포함한 많은 종류의 컴퓨팅 회로에서 기본적인 구성 요소.
• 단일 CPU, FPU 또는 GPU는 여러 개의 ALU를 포함할 수 있다.

6.조합 논리(Combinational Logic)를 표현하는 방법

• 텍스트 설명( Text Description ):
  • 조합 논리 회로의 기능과 구조를 글로 설명. 
• 회로도( Circuit Diagram ):
  • 조합 논리 회로를 시각적으로 표현한 도면. 
• 트랜지스터와 전선( Transistors and wires ):
  • 실제 조합 논리 회로를 구현할 때 사용되는 물리적 요소들. 
• 논리 게이트( Logic gates ):
  • AND, OR, NOT 등의 기본 논리 연산을 수행하는 기본적인 빌딩 블록. 
• 진리표(Truth Table):
  • 논리 회로의 모든 가능한 입력 조합과 그에 대응하는 출력을 표로 나타낸 것.
• 불린 표현식(Boolean Expression):
  • 논리 회로의 동작을 불 대수로 표현한 것.
• 이 모든 표현 방법은 조합 논리 회로의 동작 원리와 구조를 이해하고 설명하는 데 사용.

7. 진리표(Truth Table)

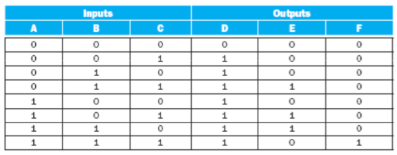
• 조합 논리(Combinational Logic, CL) 회로의 입력과 출력을 관계 짓는 표는 다음과 같은 특징을 가짐:
  • 출력은 현재의 입력에만 의존.
  • 고전압/저전압 대신 0과 1의 추상화를 사용하여 입력과 출력을 표현.
  • 입력의 모든 가능한 조합에 대한 출력을 보여줌.
• 표의 크기는 얼마나 될까?
  • N개의 입력이 각각 0 또는 1의 값을 가질 수 있으므로, 입력의 가능한 조합은 (2^N)개.
    • 따라서, 이 표는 (2^N)개의 행을 가짐.

8. Logic Gates

• 논리 게이트는 디지털 회로에서 기본적인 연산을 수행하는 전자 소자.
• 각각의 논리 게이트는 특별한 이름과 기호를 가지고 있으며, 다음과 같은 주요 논리 게이트들이 있다:
  • NOT 게이트 (또는 인버터):
    • 단일 입력의 반대 값을 출력.
    • 삼각형 모양에 원이 붙어 있는 형태로 표현.
  • AND 게이트:
    • 두 입력이 모두 1일 때만 출력이 1이 된다.
      • 기호는 일반적으로 평행한 두 선으로 끝나는 반원 모양.
  • OR 게이트:
    • 두 입력 중 하나라도 1이면 출력이 1이 된다.
    • 기호는 외곽선이 좀 더 복잡한 반원 모양으로, AND 게이트와는 구별.
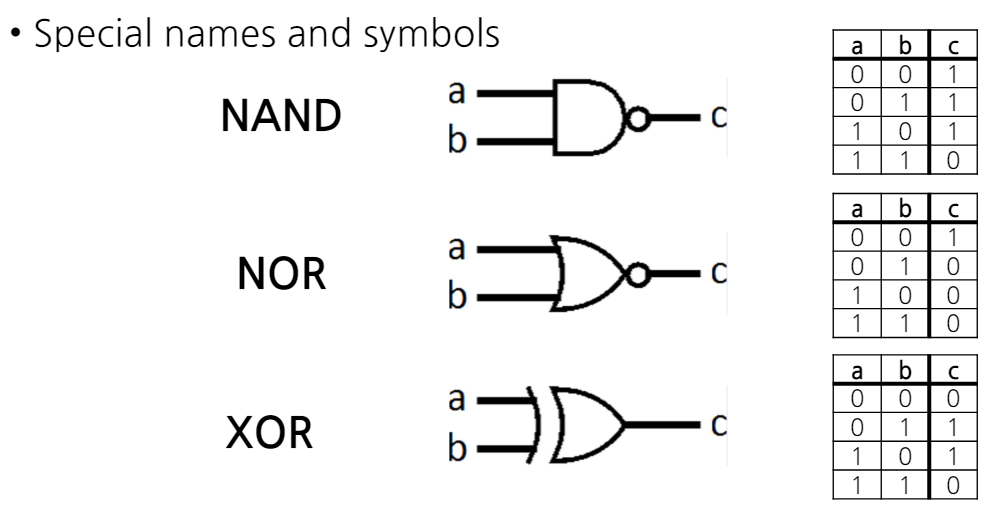
  • NAND 게이트:
    • AND 게이트의 출력을 반전시킨 것.
    • AND 게이트 기호에 원이 추가.
  • NOR 게이트:
    • OR 게이트의 출력을 반전시킨 것.
    • OR 게이트 기호에 원이 추가.
  • XOR 게이트 (배타적 OR):
    • 두 입력이 서로 다를 때만 출력이 1이 된다.
    • OR 게이트 기호에 추가 선이 그려진 형태로 표현.
  • XNOR 게이트 (배타적 NOR):
    • XOR 게이트의 출력을 반전시킨 것.
    • XOR 게이트 기호에 원이 추가.
• 이러한 논리 게이트들은 디지털 회로 설계에 있어서 기본적인 구성 요소로 활용.

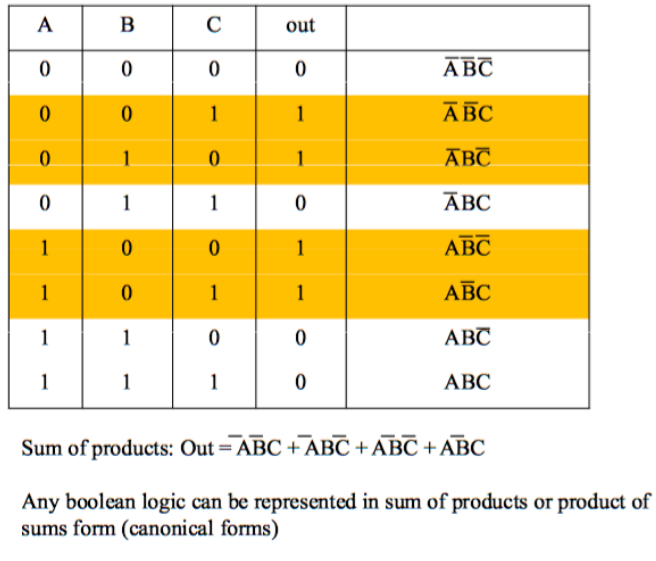
9. Truth Tables to Logic Equations

10. Laws of Boolean Algebra